В прошлых статьях мы писали о том, какие факторы влияют на величину страхового запаса и о том, как сэкономить на страховом запасе. В текущей публикации поговорим о том, нужно ли вообще отдельно считать страховой запас.
На первый взгляд вопрос достаточно смелый. Но, даже, если нам удалось оптимизировать страховой запас и снизить затраты компании, мы по-прежнему вынуждены оперировать двумя разными величинами. А значит вероятность ошибки возрастает и увеличивается риск получить перезатаренность складов или наоборот дефицит.
На одной чаше весов у нас прогноз спроса, в который мы стараемся попасть. На другой чаше весов - страховой запас, точность которого обычно не оценивается. Для многих может быть открытием, но величина страхового запаса для не продуктового сегмента может составлять до 60-70% от общего уровня запасов. И в лучшем случае страховой запас рассчитывается по нормальному распределению, которое подходит только для 4-6% ассортимента продуктового супермаркета. Это, как правило, товары, которые имеют регулярный спрос. Для всех остальных товаров оно мало применимо (см. научную справку) и перекос в ту или иную сторону может быть очень значительным.
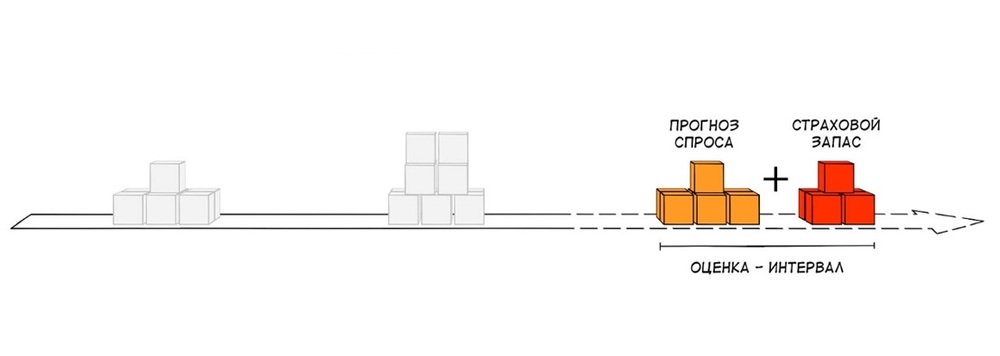В итоге у нас появляются две проблемы:
- Насколько точно спрогнозируем спрос?
- Насколько точно посчитаем страховой запас?
Как мы можем решить эти проблемы?
Нас, как специалистов по управлению товарными запасами мало интересуют эти две отдельные величины. Нас должен волновать вопрос “Сколько в целом товара нужно хранить на складе, чтобы обеспечить спрос?” Идеальным решением было бы иметь ответ на вопрос в виде одной величины без необходимости делить ее на составляющие, которые к тому же рассчитываются по разному. Это порождает только дополнительную неопределенность при планировании запасов.
Что будет, если мы будем оперировать только одним понятием - оптимальный запас?
Мы избавимся от понятия ошибки прогнозирования, которое само по себе очень мало говорит об эффективности планирования запасов. У нас останется только одна величина. Она по-прежнему останется неопределенной. Но при этом будет гораздо ближе к предметной области, чем прогноз спроса, методы расчета которого были заимствованы из отдельных областей математики и статистики и мало подходят для реальной экономики.
Важно также понимать, что в классическом варианте прогноз спроса представлен в виде одного числа. Например, 23,5 сникерса или 37 упаковок молока. Но это, как правило, случайные величины. Никто не может точно угадать, какой будет завтра или на следующей неделе спрос. И оценивать его одним числом - значит заведомо ошибаться. Об этом нужно всегда помнить.
Какая альтернатива? Использовать не одно число, а набор распределения вероятностей спроса. Для лучшего понимания проведем аналогию с прогнозом погоды. Можно заметить, что синоптики никогда не используют точные значения. Они понимают, что предсказать достоверно прогноз погоды невозможно. Вы никогда не услышите: “Завтра будет дождь, а послезавтра солнечно”. Вместо этого обычно используют вероятностный прогноз: “С 10% вероятностью завтра пойдет дождь”. И каждый уже может оценить, насколько критичны для него эти 10% - нужно ли подстраховаться и взять с собой зонт?
Такой же подход можно использовать и при планировании товарного запаса. Нужно ли подстраховаться и положить на склад дополнительно 20 бутылок молока, если вероятность продать их равна 10%?
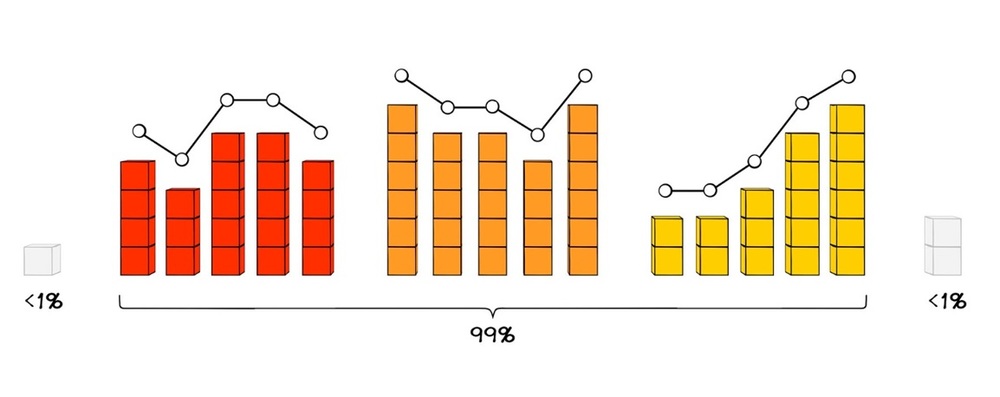Самое важное здесь - осознать переход от одной величины, которую, как нам кажется мы можем предсказать, к модели, когда вариантов развития ситуации может быть много. В первом случае мы предполагаем, что это известная цифра и её можно угадать. А на тот случай, если не угадали, будем хранить страховой запас, который считается по нормальному распределению и по распределению Пуассона. Во втором случае, мы понимаем, что может быть огромное количество вариантов развития ситуации и нельзя угадать какое-то единственное правильное число. Зато мы может рассчитать вероятность развития той или иной ситуации, а соответственно и того, какой будет спрос.
Такой подход уже более 15 лет активно применяется в управлении запасами на западном рынке, а последнее время набирает обороты и на российском. Называется этот метод - вероятностное прогнозирование спроса.
Суть метода заключается в том, что на выходе мы имеем не одно число, а набор значений - возможных объемов спроса. Например, для расчета спроса молока на день мы можем получить такие значения:
- 1 бутылку мы продадим с 10% вероятностью,
- 2 бутылки мы продадим с 30% вероятностью
- 5 бутылок мы продадим с 20% вероятностью
- 7 бутылок мы продадим с 40% вероятностью
На входе такие модели требуют задать уровень сервиса, который нужно обеспечить. О том, что это такое читайте в статье “Что такое уровень сервиса и почему он важен”.
Одно из главных преимуществ вероятностных моделей - они не привязаны к нормальному распределению. Такие модели для каждого товара строят собственное распределение объемов спроса, а значит больше подходят для применения в реальных рыночных условиях постоянных рисков и неопределенности спроса.
Используя описанную выше модель можно перейти от расчета прогноза спроса и страхового запаса к понятию оптимального запаса. О том, как это работает на практике и какие предоставляет преимущества перед классическими методами, читайте в статье “Вероятностное прогнозирование”.
Хотите узнать, как это работает в вашей сфере? Оставьте заявку внизу страницы и мы поделимся кейсами.
