Вероятностные модели – самое передовое поколение алгоритмов прогнозирования спроса. Их применение стало возможным относительно недавно, в 2015 году, вследствие быстрого роста вычислительных мощностей.
Для описания вероятностного метода прогнозирования лучше всего провести аналогию с классическими методами прогнозирования спроса, такими как метод Хольтса-Уинтерса, Простая скользящая средняя, Экспоненциальное сглаживание и др. В отличие от них результатом работы алгоритма будет не прогноз в виде одного числа, а набор распределения вероятностей: 10 тысяч единиц продукции будет продано с вероятностью 5%, 15 тысяч единиц – с вероятностью 10% и так далее. В итоге будет получено полное представление о распределении спроса.
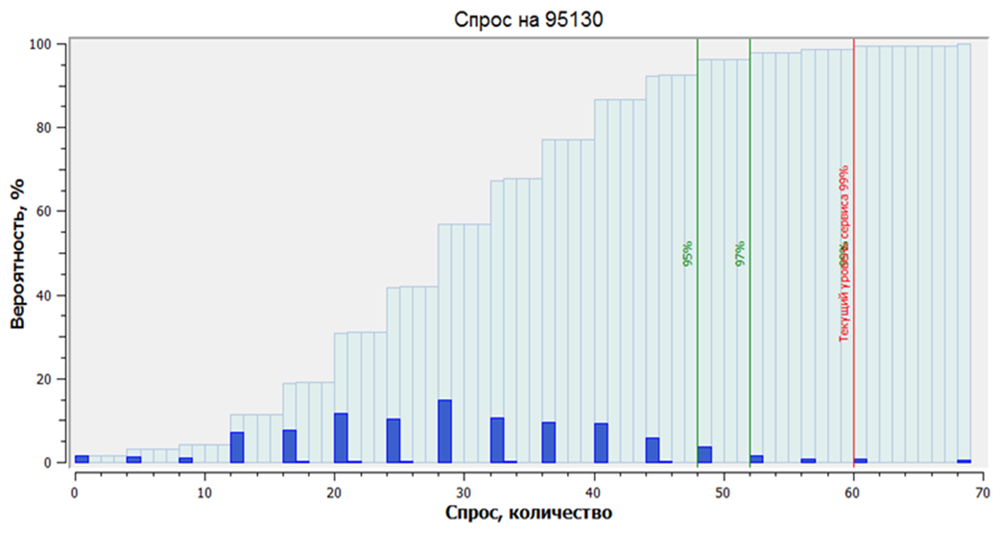
На рисунке ниже изображено построение вероятностного прогноза. Темно-синим цветом изображены вероятности возникновения тех или иных объемов спроса на позицию 95130.
В основе вероятностного метода прогнозирования лежит математическое моделирование самого процесса спроса и вероятности возникновения его объемов в прогнозируемый период. Это выгодно отличает такие модели от всех вышеперечисленных, так как последние были разработаны для решения обобщенных задач из других областей математики и статистики.
Математическая модель, используя прошлую статистику, строит такое распределение спроса (оценку вероятности спроса) для каждой товарной позиции из каждого филиала. Как показывает практика, полученное распределение практически никогда не бывает Нормальным, которое обычно используется для расчета страхового запаса в классических моделях.
Частичное вероятностное прогнозирование
Использование частично-вероятностных методов стало возможно в 2015 году. Приставка «частично» означает, что не рассматриваются мельчайшие вероятности с долей <1%. Это было связано с ограничениями производительности серверов и стационарных компьютеров. Тем не менее такой подход дает большие возможности для управления спросом. Можно самостоятельно управлять уровнем сервиса, то есть находить оптимальный баланс между тем, сколько спроса нужно удовлетворить и сколько товаров хранить на складе в каждый момент, чтобы максимизировать прибыль. Соответственно, понятие страхового запаса становится уже неактуальным.
Как работает метод вероятностного прогноза на практике?
Допустим, необходимо спрогнозировать спрос для 10 000 000 SKU. У нас имеется математическая модель, которая умеет моделировать спрос на основе прошлой статистики продаж. На основании параметров спроса создается математическая модель, которая описывает характеристики спроса. Например, вероятность возникновения различных объемов, вероятность возникновения или отсутствия спроса на протяжении нескольких дней, недель или месяцев. Далее она делает от 500 тыс. до 1 млн прогнозов для каждой товарной позиции, моделируя возможные варианты развития событий в будущем. В итоге в зависимости от частоты возникновения того или иного объема спроса в моделируемых реальностях на выходе мы будем иметь распределение вероятностей:
- 15 штук товара будет продано с 20% вероятностью
- 17 штук товара будет продано с 40% вероятностью
- 25 штук товара будет продано с 30% вероятностью
- 30 штук товара будет продано с 10% вероятностью
Теперь нет необходимости отдельно рассчитывать страховой запас. Вместо него используется оптимальный запас в соответствии с уровнем сервиса. На рисунке ниже темно-синими цветом изображены вероятности возникновения объемов спроса. Если задача состоит в том, чтобы обеспечить уровень сервиса первого рода 95%, то нужно найти ту точку, где суммарно находится 95% возможных объемов спроса. На графике ниже видно, что эта точка соответствует 49 единицам товара. То есть именно столько нам необходимо хранить в данный конкретный момент.
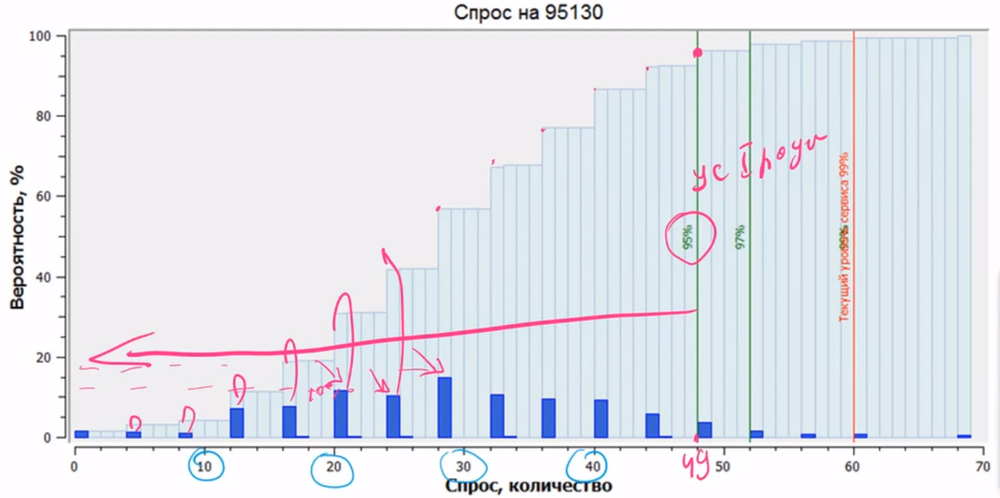
Частично вероятностное прогнозирование уже позволяет переходить к понятию рисков, оперировать понятиями возможности возникновения того или иного объема. Если мы знаем эти вероятности и объемы, то уже можем оценивать рентабельность нашего запаса: какие товарные позиции выгодно хранить, где выгодно удовлетворять спрос, а где это несет больше убытков, чем прибыли. Здесь появляется финансово-рисковая модель.
Полное вероятностное прогнозирование
В 2018 году широкое применение получили полновероятностные модели. Они способны учитывать даже самые малые вероятности распределения спроса вплоть до 0,01%, что может быть весьма существенным при больших объемах. Поэтому не рекомендуется ими пренебрегать. Подробнее о том, почему важно учитывать маловероятные события, читайте в статье «Почему важно думать вероятностно?»
Важное отличие полновероятностных методов – возможность получить вероятностную оценку не только объемов спроса, но и других параметров. Один из них – остаток товаров, который будет на складе к моменту поступления заказа. В классических методах для этого используется точечная оценка. Например, по средним продажам может быть рассчитан объем товаров на предполагаемую дату. В таком подходе никак не учитываются риски: срыв сроков поставки товаров, которые уже едут от поставщика, возможные всплески, колебания спроса.
Другими величинами, которые можно оценивать с помощью вероятностей, могут быть смещение сроков поставки, возникновение дефицита, эффективность маркетинговой акции и так далее. Чем больше величин, где присутствует неопределенность, можно оценивать с помощью распределения вероятностей, тем более точнее и эффективнее можно управлять товарными запасами и рисками.
Следующий этап развития полновероятностных моделей – сквозное моделирование всей цепочки поставок от распределительного центра до торговых точек или потребителей. При этом учитываются распределение вероятностей сроков доставки между всеми звеньями цепи, вероятность остатков на момент доставки, вероятность сбоев поставки и прочие факторы. В противовес обычному сложению очищенных историй продаж сквозное моделирование позволяет учитывать сроки доставки и смещение горизонтов планирования в связи с удаленностью складов, а также начальные и прогнозируемые остатки филиалов без необходимости прибегать к упрощению (сложению всех остатков), что некорректно.
Финансово-рисковая модель
Дополнительное преимущество вероятностных методов – возможность использования финансово-рисковой модели. Она позволяет понять, какой объем запасов экономически целесообразно хранить на складе. Выгодно ли поддерживать уровень сервиса 95% для этой конкретной позиции, либо затраты на ее хранение будут выше дохода, который мы получим от реализации? Если вероятность продаж очень мала, и есть риск, что деньги будут заморожены в активах на складе, то нужно ли закупать товары или рискнуть и не инвестировать деньги в запас?
Будущее непредсказуемо, поэтому нельзя прогнозировать спрос без учета рисков, хотя классические модели работают именно так. Построенная ими модель может выглядеть подобным образом:
В реальной жизни компания сталкивается с тем, что для разных товаров возникает множество разных рисковых ситуаций, которые в совокупности могут очень сильно влиять на оптимальный товарный запас.
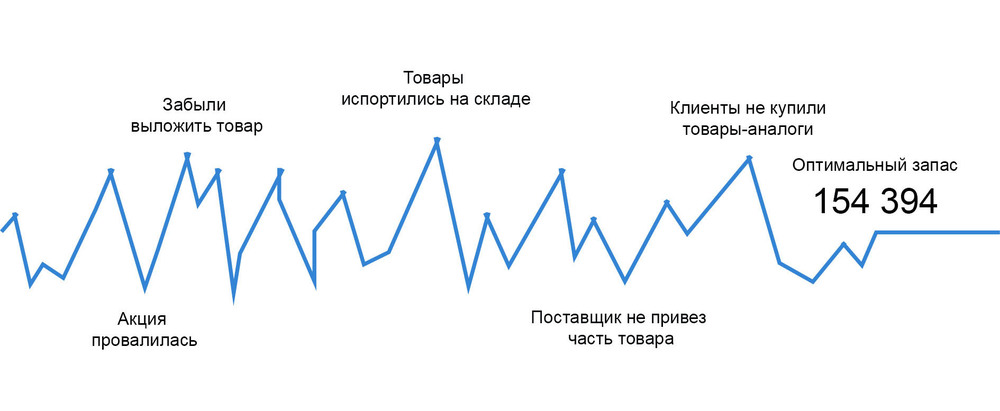
Вероятностные алгоритмы в совокупности с финансово-рисковой моделью просчитывают множество вариантов развития ситуаций в будущем, учитывают при этом возможные риски. В конечном счете применение такой модели определит оптимальный товарный запас для каждой позиции, чтобы потери компании были минимальны.
Пример расчета оптимального товарного запаса. Синим выделен объем, который максимально рентабелен для компании на текущий момент, в текущих рыночных условиях:
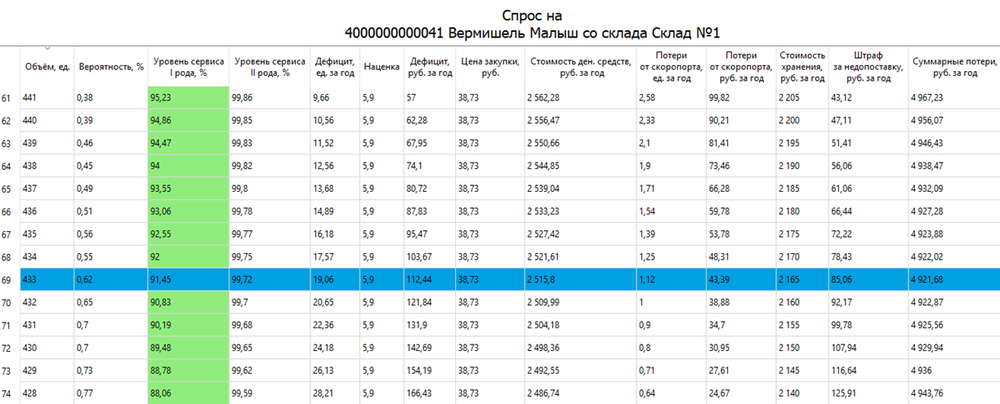
См. также:
Научная справка о непременимости классических методов для прогнозирования редкого спроса
Обзор других методов:
- Экспоненциальное сглаживание (1-2 поколение);
- Простая скользящая средняя (SMA, Simple Moving Average) (1-2 поколение);
- Метод Хольта-Винтерса (1-2 поколение);
- Авторегрессия (1-2 поколение);
