
Обновление статьи от 25.05.2023. На сегодняшний день в связи с развитием технологий и вычислительных мощностей мы считаем, что эффективнее всего сразу моделировать заказ поставщику, а не прогнозировать отдельно товарный запас. Подробнее об этом читайте в статье «Почему нужно сразу моделировать заказ, а не прогнозировать отдельно спрос и запас?». При этом вся информация в статье о преимуществах прогноза товарного запаса перед прогнозом спросом актуальна.
Большинство российских компаний управляют запасами с помощью методов классического прогнозирования спроса – таких, как экспоненциальное сглаживание, ARIMA, скользящая средняя, метод Хольта-Винтерса и другие. Проблема не только в том, что все эти методы устарели и плохо предсказывают спрос для большинства товарных позиций. Все они отвечают только на один вопрос: каким будет спрос в следующем периоде?
Мы привыкли считать, что прогноз спроса – основной фактор, который нужен, чтобы грамотно управлять запасами. Причем чем точнее прогноз, тем лучше. Но когда мы фокусируемся исключительно на спросе, мы упускаем из вида цель. Нам нужно знать, сколько товара хранить, чтобы получить максимальную прибыль и минимальные убытки.
В статье мы расскажем:
- как работают классические методы управления запасами
- какие проблемы возникают, если в расчетах мы ориентируемся только на прогноз спроса
- почему важно перейти от прогнозирования спроса к прогнозированию товарных запасов
- как работают вероятностные алгоритмы прогнозирования.
Как работают классические методы управления запасами?
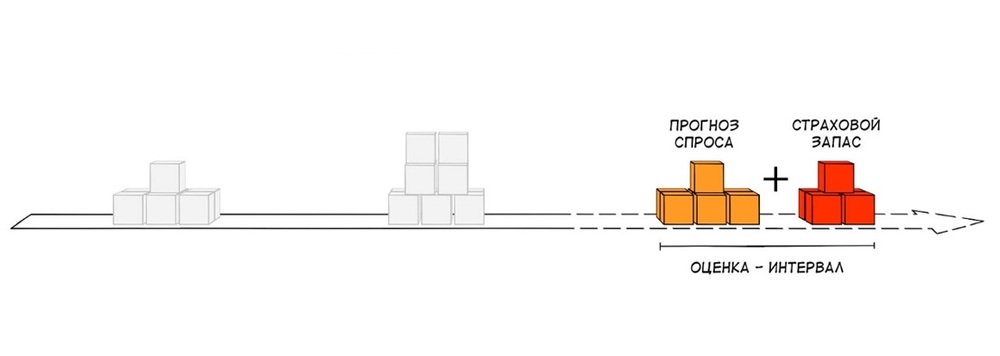
Все классические алгоритмы рассчитывают необходимый товарный запас по одному принципу. Они прогнозируют спрос на основе истории продаж – например, с помощью скользящего среднего. Получают какое-то число, сверху добавляют страховой запас.
Не все учитывают, что история продаж не отражает реальный спрос – она искажена дефицитами, воздействием маркетинговых акций, аномальными продажами. Получить корректный прогноз спроса на основе такой истории невозможно. Мы подробно рассказали об этой проблеме и способах решения в статье «Как подготовить историю продаж, чтобы получить корректный прогноз спроса?».
Основная проблема этих методов в том, что мы получаем результат в виде одной цифры. Например, на следующей неделе у нас купят 24 единицы товара. Насколько точен этот прогноз? В реальных рыночных условиях никто не может точно угадать, каким будет спрос завтра или на следующей неделе. Оценивать спрос одним числом – заведомо ошибаться.
Страховой запас добавляют как раз для того, чтобы снизить риск последствий из-за неточного прогноза. Иногда его объем составляет до 70% от общего объема запасов. В классических методах страховой запас рассчитывают с использованием Нормального распределения или распределения Пуассона. Доказано, что эти распределения не описывают спрос для 94% товарных позиций.
Кроме того, доказано, что классические методы прогнозирования не работают для товаров с редким спросом (см. научную справку в конце статьи).
Чтобы определить, редкий или гладкий спрос у товара, считают среднее расстояние в днях между соседними фактами продаж. Если это число больше 1.25 дней, то перед нами редкий спрос, если меньше – гладкий.
К товарам с разреженным спросом относятся автозапчасти, электротовары, стройматериалы, канцелярия, бытовая химия, термотехника. Считается, что у продуктов питания гладкий спрос. Но на самом деле 94% товаров продуктового ассортимента и до 99% остальных товаров имеют разреженный спрос.
Предсказывать спрос для таких товаров в виде одной цифры – все равно что вслепую стрелять по цели, которая постоянно движется и меняет размеры.
Что происходит, если мы оперируем только прогнозом спроса для управления запасами?
Спрос – это еще не все. Кроме спроса, нам нужно учесть:
- риски дефицита, недопоставки, смещение срока поставок
- промоакции
- сезонность и праздники
- остатки на дату поступления
- затраты на хранение товара
- убытки – например, просрочка или пересортица
- стоимость альтернативных вложений.
Некоторые факторы определены заранее. Другие мы не знаем – например, вероятность дефицита или недопоставки. Да и прогноз спроса на конкретный день в следующем периоде – величина неопределенная.
Оперируя только спросом, мы не учитываем возможные потери
Чтобы грамотно управлять запасами, мы обязаны учитывать риски потерь – просрочек, недопоставок, дефицитов, аномального спроса. Классические модели прогнозирования спроса не учитывают их вероятность.
Если при управлении запасами мы опираемся только на прогноз спроса, то считаем, что все пройдёт идеально:
- Товар доставят вовремя и в полном объёме.
- Не случится ни пересортицы, ни порчи товаров.
- Товар будет выложен на полку.
- Спрос будет соответствовать прогнозу.
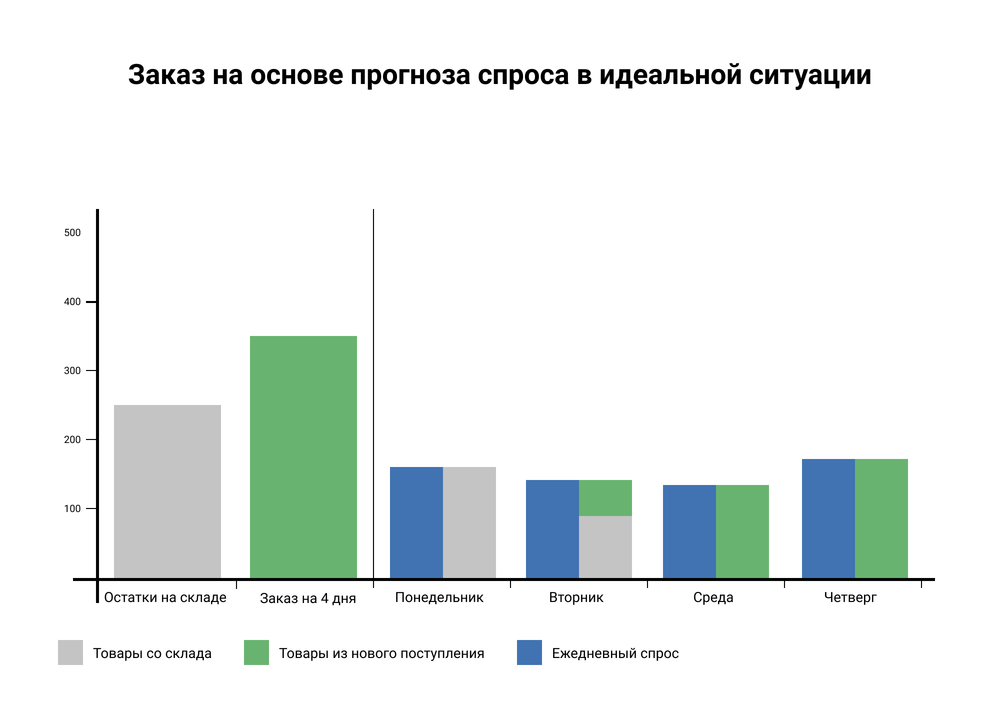
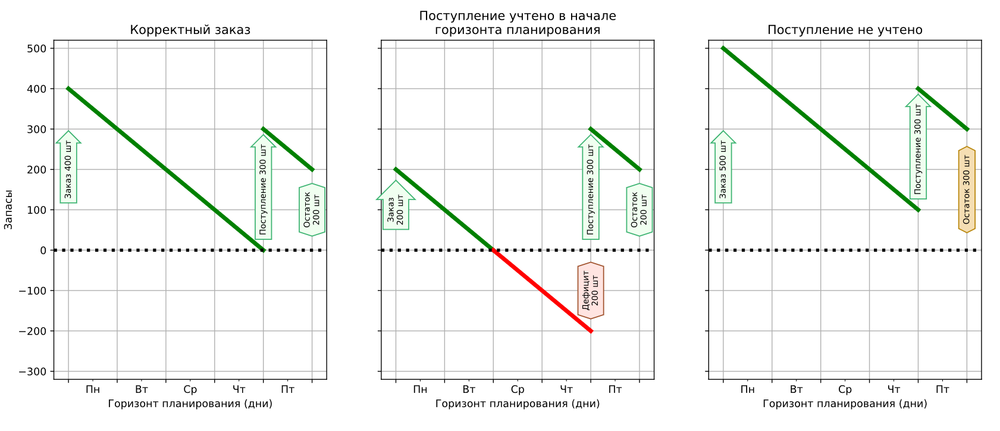
На картинке ниже ежедневный спрос у товара – 150 единиц, на складе осталось 250 единиц. Заказ на четыре дня на основе прогноза спроса – 350 единиц. Спрос у товара гладкий, не произошло никаких неожиданностей, и заказа хватило на весь расчетный период.
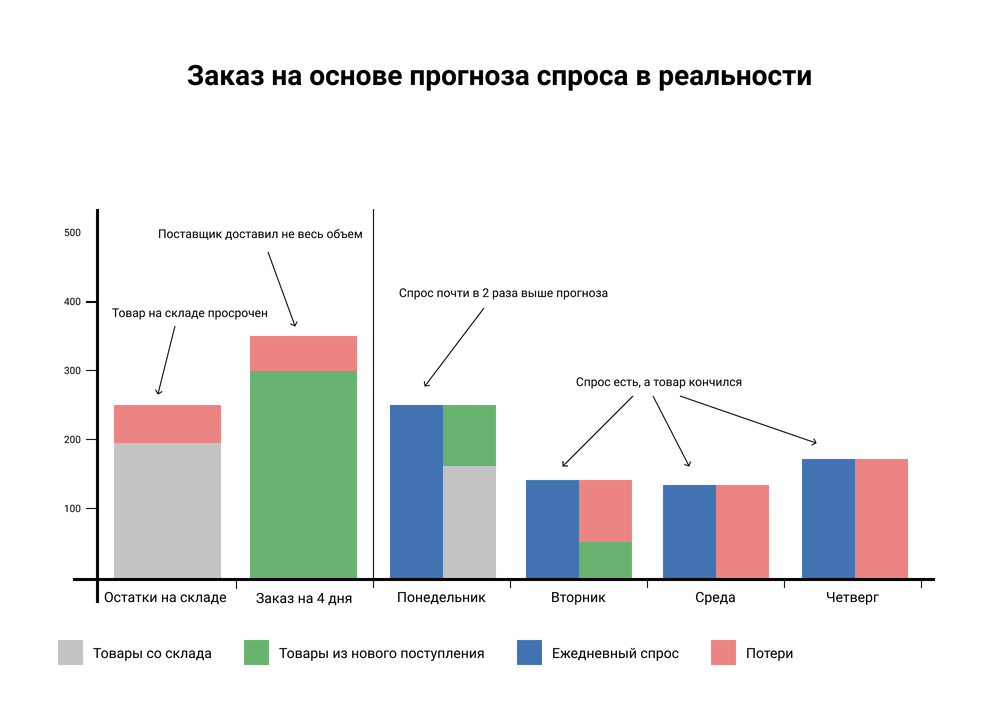
Но в жизни не все идет по плану. Постоянно происходят разные события, случайные и запланированные, которые влияют на спрос и на объем запасов. Поставка может задержаться, товар на складе может оказаться просроченным. Может произойти внезапный всплеск спроса, и наших запасов не хватит на следующие дни, случится дефицит. Либо, наоборот, покупатели перейдут к конкурентам.
Если мы не учитываем вероятность этих событий, а учитываем только спрос, то не можем точно знать, сколько товаров будет у нас на складе такого-то числа. При таком подходе расчеты заказов будут некорректными.
Если у нас стабильные, регулярные ежедневные продажи и большой горизонт планирования, мы можем управлять запасами, учитывая только спрос. Но в современных рыночных условиях такого практически не бывает.
Не учитываются будущие поступления товаров
Чтобы корректно рассчитывать заказы, мы должны учесть не только риски, но и будущие поступления товаров.
Как рассчитать заказ, если мы знаем только прогноз спроса на период? Если на этот период нет поступлений, то мы просто вычитаем из прогноза спроса остатки на складе и делаем заказ на полученное количество товара. А если в пути уже находится какой-то заказ?
Допустим, мы рассчитываем заказ на период длиной в пять дней. У товара постоянный спрос – 100 единиц в день. По нашим расчетам, в начале периода на складе будет пусто, но на пятый день ожидается поступление 300 единиц товара. Будем считать, что запас становится доступным в день поступления.
Для покрытия спроса нам потребуется 400 единиц товара к началу периода. Потом мы сможем расходовать запас из поступления. В итоге в конце недели у нас останется 200 единиц товара.
Если при расчете заказа мы оперируем только прогнозом спроса, у нас есть два варианта: учесть будущее поступление так, как будто оно уже находится на складе, или не учитывать его вообще. В первом случае мы закажем 200 единиц и уйдем в дефицит на 3 и 4 день. Во втором случае мы закажем 500 единиц, в конце недели останется 300, а это грозит перезатариванием склада.
Оба варианта имеют свои недостатки. В реальных условиях с ежедневными поставками и большим количеством SKU такой подход может привести к большим финансовым потерям. А если мы будем прогнозировать спрос на более короткий период, то придется держать избыточный товарный запас. Это тоже достаточно затратно.
Чтобы сделать корректный заказ (в примере это 400 единиц), нужно понять, спрос на какие дни покрывается будущим поступлением, и сделать заказ только на оставшиеся дни. Если спрос у товара постоянный, мы можем просто разделить объем спроса на количество дней.
Но в реальной ситуации все намного сложнее. Спрос внутри периода отличается из-за внутринедельной сезонности, маркетинговых акций или других факторов, так что делить его пропорционально числу дней некорректно. Учитывать приходится десятки или сотни поставок в разные дни. Запасы на складе могут состоять из нескольких партий с разным сроком годности. Остатки на складе постоянно меняются, и прогноз спроса сам по себе не помогает отслеживать эти изменения.
Для полноценного управления мы должны прогнозировать товарные запасы, а не спрос
Мы не можем делать точные заказы только на основе прогноза спроса. Нам нужен алгоритм, который умеет моделировать движение остатков на складе по дням с учетом всех поставок. Мы должны включать в расчеты возможные потери, связанные с дефицитом, вероятности аномально больших продаж либо, наоборот, ухода покупателей в другой магазин из-за маркетинговой акции. Если же мы планируем акцию, мы должны учесть скачок продаж и естественный спад после ее окончания.
Когда мы начинаем учитывать все это, то от прогнозирования спроса переходим к прогнозированию объема товарных запасов на складе в любой день в будущем. Превосходство такого подхода к управлению очевидно. Если мы знаем вероятный спрос и можем спрогнозировать объем запасов на определенную дату, то более точно рассчитаем, сколько нужно заказать, чтобы получить максимальную выгоду.
Как вероятностные алгоритмы прогнозируют товарные запасы?
В России вероятностные алгоритмы почти не используются, хотя в западной практике они считаются самым прогрессивным методом для управления товарными запасами. С помощью вероятностных методов прогнозирования 4-го поколения мы можем прогнозировать запас всего ассортимента вплоть до группы Z.
Как это работает?
Вероятностные алгоритмы выдают прогноз спроса в виде распределения вероятностей.
Вместо одного прогноза модель делает более ста тысяч прогнозов для товарной позиции. Затем подсчитывает, сколько раз возникал тот или иной объем продаж в моделируемых реальностях, и выдает прогноз в виде распределения вероятностей для разных объемов.
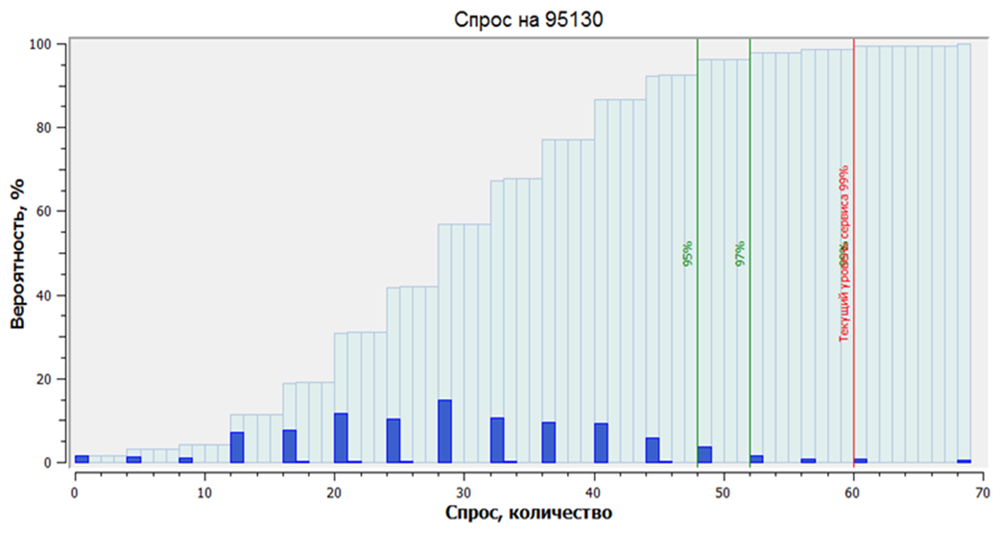
Такой алгоритм хорошо работает для всех товаров, включая товары с редким или вариативным спросом. Мы получаем не одну цифру с низкой точностью, а ряд вероятностей. Например, вероятность продажи 12 единиц товара в день составляет 7,5%. А продать 20 единиц мы сможем с 15% вероятностью.
Больше не нужно вычислять страховой запас. Мы можем заранее определиться с целевым уровнем сервиса и сразу закупить нужное количество товара. На картинке ниже из распределения вероятностей продаж мы делаем вывод: чтобы покрывать 95% случаев возможного спроса (обеспечивать уровень сервиса первого рода 95%), нужно хранить 49 единиц.
Вероятностные алгоритмы считают вероятности потерь и включают их в прогноз
Для вероятностных алгоритмов прогноз спроса – только один из шагов для расчета нужного товарного запаса. Кроме вероятностей разных объемов спроса, алгоритмы подсчитывают и вероятности возникновения разных потерь. Оптимальный уровень сервиса для каждого товара подсчитывается на лету.
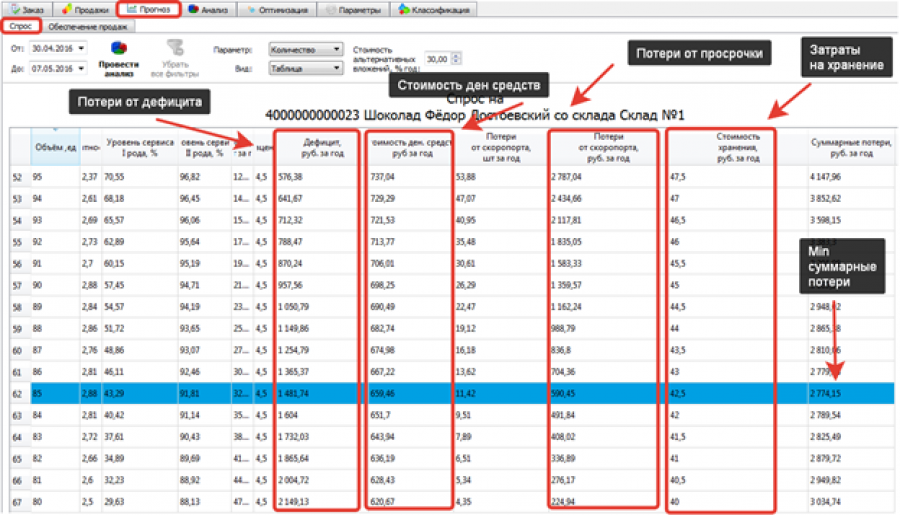
На картинке мы видим, что программа учла различные факторы, смоделировала оптимальный товарный запас для выбранной товарной позиции и рассчитала, что оптимальный уровень сервиса составляет 91,81%. Именно при таком уровне сервиса возможные потери будут сведены к минимуму.
Вероятностные алгоритмы моделируют ежедневный товарный запас с учетом дат поступлений
Вероятностные алгоритмы, реализованные в Forecast NOW!, моделируют, как будут изменяться остатки на складе в произвольные периоды. Программа прогнозирует, сколько товара будет храниться на складе в конкретный день, какой будет спрос и хватит ли запасов для покрытия этого спроса. Результаты также описываются в виде распределения вероятностей.
Программа определяет вероятность, что возникнет дефицит того или иного объема, на основе огромного массива данных из более 100 000 возможных вариантов развития событий. Учитывается уровень сервиса, другие параметры и ограничения, и рассчитывается оптимальный заказ.
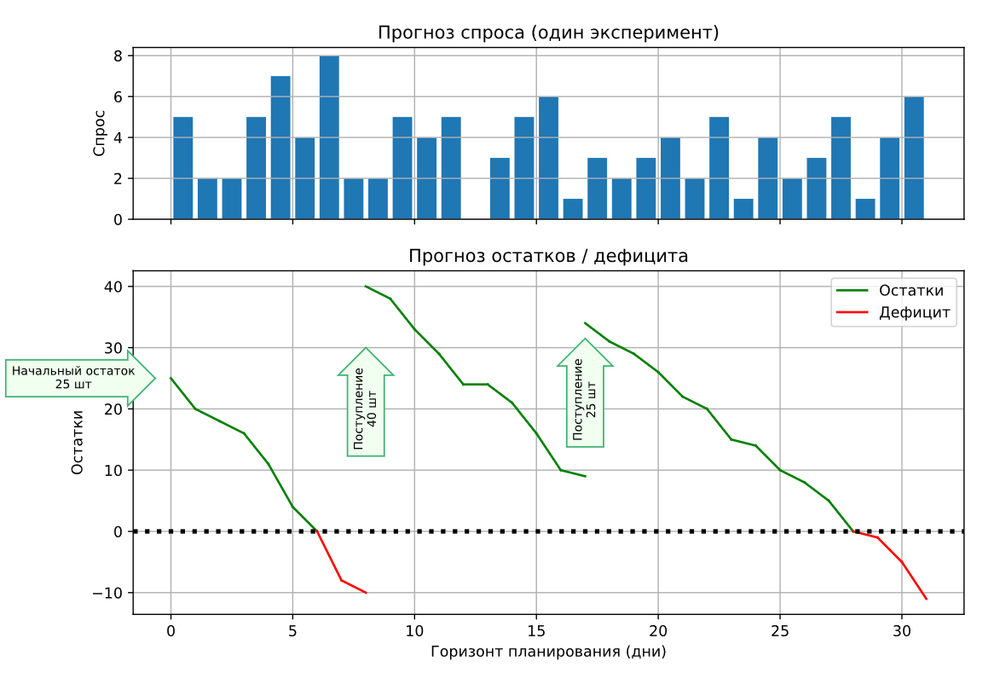
На картинке алгоритм смоделировал движение остатков на складе для одного эксперимента. Более подробно о работе модели читайте в статье «Алгоритм вероятностного подневного моделирования запасов с учетом дат поступлений».
Вывод
- Чтобы грамотно управлять товарными запасами, недостаточно знать только прогноз спроса. Мы рассчитываем прогноз для того, чтобы узнать, какой оптимальный запас нужно хранить.
- Разреженный спрос нельзя прогнозировать одним числом, из-за неточности прогноза мы будем вынуждены хранить слишком большой страховой запас.
- При расчете оптимального запаса необходимо учитывать возможные потери, будущие поступления и ежедневное изменение остатков на складе.
- Вероятностные алгоритмы вместо одной цифры дают прогноз спроса в виде распределения вероятностей. Это расширяет возможности управления запасами.
- Кроме спроса, вероятностные модели Forecast NOW! прогнозируют возможные потери, учитывают новые поступления и моделируют товарные запасы по дням.
- Вероятностные алгоритмы Forecast NOW! учитывают множество факторов: нестабильность поставок, влияние маркетинговых акций, убытки от дефицита, затраты на хранение запасов и так далее. В итоге вы получаете расчет товарного запаса, оптимального с финансовой точки зрения.
Научная справка. О неприменимости классических методов для прогнозирования редкого спроса
Одним из первых методов, применявшихся для прогнозирования спроса на основании временных рядов, является метод экспоненциального сглаживания[1]. Этот метод может использоваться для прогнозирования равномерного спроса.
В 1972 году Кростон[2] показал, что для прогнозирования прерывистого спроса в общем случае модель экспоненциального сглаживания не является адекватной, и предложил свою модель, в которой отдельно прогнозируются интервалы между покупками и их объемы.
В работе 2001 года[3] было показано, что оценки метода Кростона являются смещёнными, и был предложен усовершенствованный вариант этой модели.
Метод экспоненциального сглаживания опирается на предположение о стационарности временного ряда. В случае наличия тренда требуется его обобщение. Линейный метод Холта[4] опирается на оценку локального среднего значения и скорости роста.
Другим вариантом учёта тренда является использование скользящего среднего. В этом случае прогноз осуществляется не на основании всего объема исторических данных, а с использованием только наиболее свежей части данных.
Одним из наиболее распространённых вариантов обобщения моделей скользящего среднего, экспоненциального сглаживания, линейного тренда и случайного блуждания является модель ARIMA.
Рассмотренные модели были созданы в рамках параметрического подхода к моделированию случайных процессов. Они предполагают, что объемы продаж (и интервалы между ними в модели Кростона и её обобщениях) имеют известное распределение. Разработано множество модификаций этих моделей, опирающихся на использование различных классических распределений. Показано, что спрос, имеющий разряженный характер, плохо описывается с помощью классических распределений.
Практическое применение таких моделей требует анализа распределений экспертным образом в каждой конкретной ситуации и может не дать удовлетворительного результата.
Список литературы
|
[1] ↑ |
R. J. Hyndman, A. B. Koehler, J. K. Ord и R. D. Snyder, Forecasting with Exponential Smoothing: The State Space Approach, Berlin: Springer, 2008. |
|
[2] ↑ |
J. D. Croston, «Forecasting and stock control for intermittent demands,» Operational Research Quarterly, № 23, p. |
|
[3] ↑ |
A. A. Syntetos и J. E. Boylan, «On the bias of intermittent demand estimates,» International Journal of Production Economics, № 71, p. |
|
[4] ↑ |
C. C. Holt, «Forecasting seasonals and trends by exponentially weighted moving averages,» International Journal of Forecast, № 20, p. |
|
[5] |
A. A. Syntetos и J. E. Boylan, «The accuracy of intermittent demand estimates,» International Journal of Forecasting, № 21, pp. |
|
[6] |
R. D. Snyder, «Forecasting sales of slow and fast moving inventories,» № 140, pp. |
|
[7] |
L. Shenstone и R. J. Hyndman, «Stochastic models underlying Croston’s method for intermittent demand forecasting,» Journal of Forecasting, pp. |