Почему повышение точности прогноза не гарантирует повышение прибыли. Как привычный показатель вводит компании в заблуждение.

Задача прогнозирования спроса и товарных запасов неизбежно связана с оценкой точности прогноза. В российской практике этот показатель считается одним из ключевых, на который ориентируются компании. Однако, по нашему опыту, он переоценен и часто вводит компании в заблуждение относительно его влияния на конечную прибыль. В статье последовательно рассмотрим 5 основных проблем, с которыми сопряжено использование данного показателя, и предложим варианты их решения.

Прежде всего разберемся, зачем вообще считать точность прогнозирования. Ответов может быть несколько:

• Выбрать оптимальную модель прогнозирования
• Рассчитать страховой запас
• Выделить SKU, которые требуют повышенного внимания
• Сравнить разные программные продукты

Оценка точности прогноза определяется через ошибку прогнозирования. Ошибка в данном случае – это разница между фактическим значением спроса и его прогнозным значением. То есть чем больше будет ошибка прогнозирования, тем менее точен прогноз. Например, при ошибке прогнозирования 5%, точность прогноза будет составлять 95%. Но самый большой подвох, как увидим дальше, кроется в большом количестве методов расчета ошибки прогнозирования. 

В большинстве случаев точность прогнозирования выглядит так: 

98.1%

Что может скрываться за этими цифрами? Бесконечное количество метрик, которые считаются совершенно по-разному, например, таких:

 

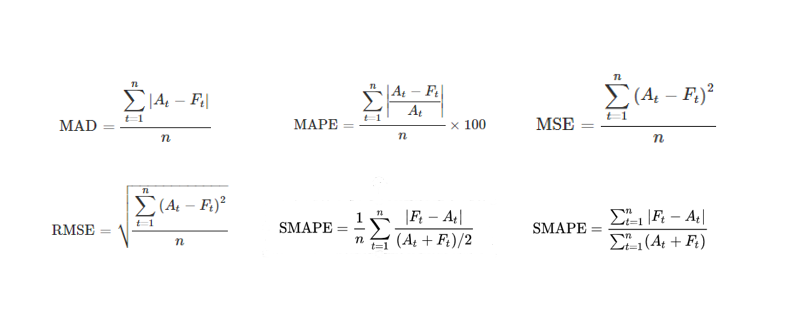
И результаты в каждом случае могут сильно отличаться. Сформулируем первую проблему использования точности прогноза как главного критерия оценки эффективности управления запасами.

Проблема 1. Ошибки прогнозирования могут считаться по разным метрикам, которые дают очень разные результаты и несравнимы между собой

Чтобы проиллюстрировать эту проблему, приведем пример:

 

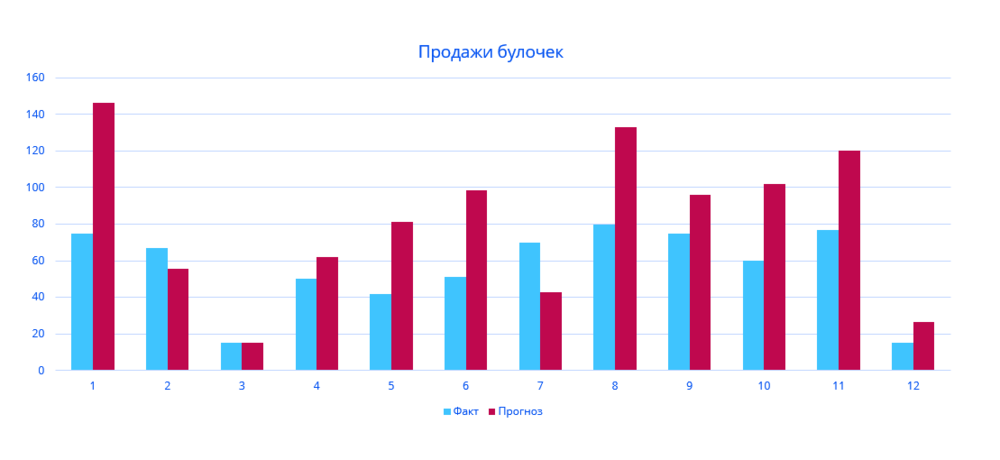На рисунке – график продаж булочек за последние 12 дней, а ниже ошибка прогнозирования, рассчитанная по различным методикам.

Как можно увидеть, точность прогноза сильно различается. И этой статистикой можно манипулировать так, как будет удобно. Взяв за основу нужную метрику, некоторые сотрудники могут предоставлять руководству те результаты, которые ожидаются. Или, например, они могут закрывать проект такими цифрами, которые выставят его в выгодном свете. А в некоторых случаях компании могут даже заниматься самообманом, не подозревая об этом и веря, что все идет хорошо. 

Решение 1. Фиксировать конкретную метрику оценки точности прогнозирования и методику расчета на уровне компании

Проблема 2. Как оценить точность прогнозирования для группы товаров и в целом для компании

Теперь эту метрику нужно как-то агрегировать на всю компания. Допустим, у нас есть 100 000 SKU, продажи которых могут кардинально различаться. Нельзя их просто усреднить. Например, у нас есть два вида товаров: виски и колбаса, которые имеют такие показатели:

Если мы сложим прогнозные и фактические продажи по этим товарам, то они друг друга уравняют. Точность прогнозирования будет 100%. Но, если смотреть этот показатель отдельно по товарам, все уже не так хорошо. 

К тому же самые внимательные могут заметить, что величина отклонения факта от прогноза у этих товаров одинаковая, но величина ошибки прогнозирования MAPE в одном случае – 50%, а в другом – 100%. Как легко догадаться, это происходит из-за того, что фактические продажи отклоняются в разные стороны. Это еще одна проблема такого подхода. О ней мы поговорим чуть ниже. 

Для решения этой проблемы можно пойти по пути взвешивания этих ошибок в соответствии с их вкладом в важные для компании критерии. Это может быть прибыль или объем продаж. 

Например, мы взвешиваем виски и спички по среднему спросу. И в этом случае ошибка сдвигается к тому товару, который больше продается. В итоге мы получаем более-менее верную оценку точности прогнозирования.

Решение 2. Использовать взвешенные ошибки по бизнес-показателям для оценки точности прогноза

Давайте теперь посмотрим на высокую и низкую точность прогнозирования с другой стороны. 

Проблема 3. Высокая и низкая точность прогнозирования не является ключевым драйвером экономической эффективности

Для многих SKU высокая или низкая точность прогнозирования не является ключевым драйвером эффективности. Не стоит рассматривать эти математические ошибки как что-то, что всегда нужно использовать для оценки качества управления запасами. Нужно понимать, что эти методы пришли из математики и предназначались именно для статистических и математических, а не экономических показателей.

Например, MAPE использовалась для прогнозирования временных рядов, которые имеют регулярное Нормальное распределение, такие как, например, потребление электроэнергии. И только после ее стали применять для оценки точности прогноза спроса. Но, когда мы говорим про продажи товаров, то Нормальное распределение имеют лишь около 6% товаров. Это, как правило, продукты питания ежедневного потребления.

Рассмотрим пример редкого спроса – бытовая химия, которая не востребована каждый день:

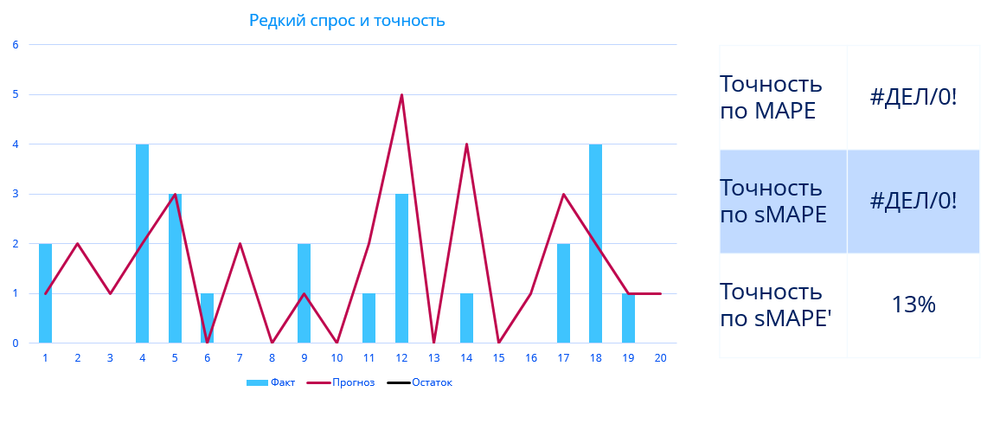
Как видно из графика, многие метрики здесь просто не работают. Точность по MAPE и sMAPE невозможно посчитать. Даже если получится как-то ухитриться и «выровнять» данные, то мы получим катастрофически низкую точность – 13%.

Теперь посмотрим на предметную область, а не просто на математические ошибки:

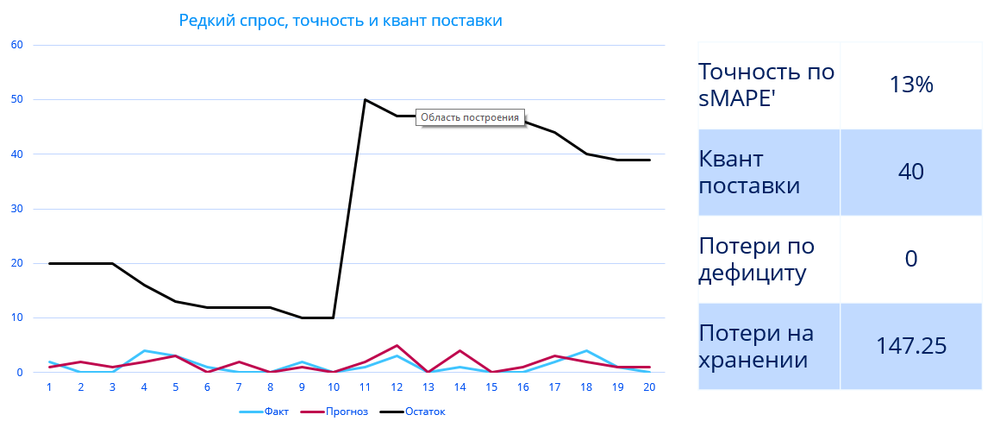
Здесь можно увидеть, что точность прогнозирования вообще ни на что не влияет, потому что остаток обусловлен минимальным квантом поставки или частотой поставки, которую может обеспечивать поставщик. Поэтому обращать внимание на эту цифру совершенно не имеет смысла. И здесь уже стоит заботиться не о повышении точности прогнозирования, а о переговорах с поставщиками. 

Дефицит в прошлом и высокая точность прогноза

С другой стороны, дефицит в прошлом тоже может вводить в заблуждение относительно точности прогноза. Он занижает продажи, а значит, точность может быть завышена или занижена. 

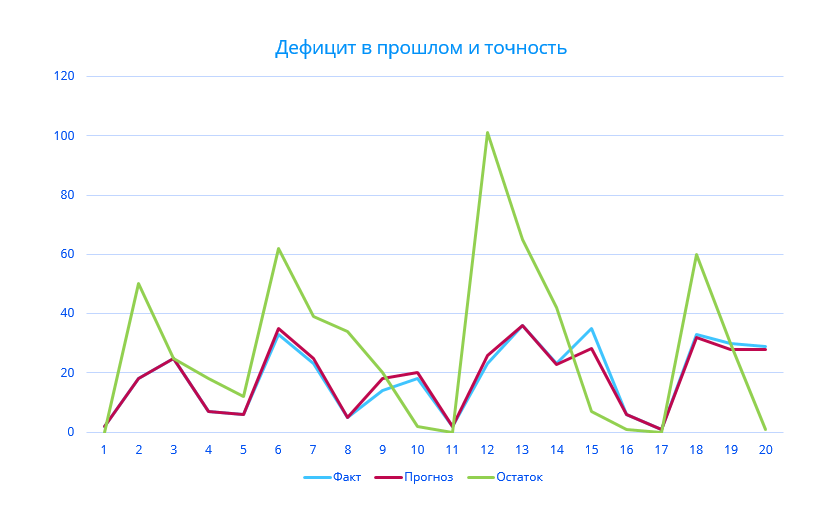
В примере точность по MAPE – 95%. Но при этом мы постоянно попадаем в дефицит, а наш прогноз недооценивает спрос в эти периоды. 

Решение 3. Оценивать точность прогнозирования оптимальных запасов и не опираться на математические ошибки

Проблема 4. MAD, MSE, RMSE, MAPE – это математические ошибки. Они ничего не говорят про деньги

Исходя из нашей практики, самым распространенным методом оценки точности прогноза является средняя абсолютная процентная ошибка (MAPE) и ее вариации. Также используются средняя абсолютная ошибка (MAE), средняя квадратичная ошибка прогнозирования (RMSE), среднее абсолютное отклонение (MAD).

Несмотря на то что большинство компаний до сих пор используют вышеописанные методы для оценки, мы считаем, что они недостаточно корректны и не подходят для применения в реальном бизнесе.

Эти методы больше относятся к математике, а не к бизнесу. Это обезличенные цифры, которые ничего не говорят про деньги. Решения же принимаются на основе выгоды, измеряемой деньгами. Например, ошибка в 80% на первый взгляд звучит устрашающе. Но в реальности за ней могут скрываться совершенно разные вещи. Ошибка по гвоздям со стоимостью одного гвоздя в 50 копеек – это одни потери. Но они совершенно несопоставимы с потерями от продажи промышленного оборудования стоимостью 700 000 рублей с той же величиной ошибки прогнозирования. Не стоит забывать и про объем, который тоже не учитывается ошибками. 

Второй важный момент – это заморозка денежных средств в запасах и недополученная прибыль от дефицита продукции на складе. Например, если мы прогнозируем продажу 20 колесных дисков, а по факту продали 15. То это одна цена ошибки – 5 колесных дисков, которые потребуют затраты на хранение на определенное время, и, как следствие, стоимость замороженных оборотных средств под определенный процент. Если рассмотреть обратную ситуацию – прогнозируем продажу 20 дисков, спрос составляет 25 штук. Это уже упущенная прибыль, которая составляет разницу сумм закупки и реализации продукции. По сути, мы имеем одну и ту же ошибку прогнозирования, но результат от нее может быть совершенно разным.

Давайте посмотрим на пример со списанием просроченной продукции:

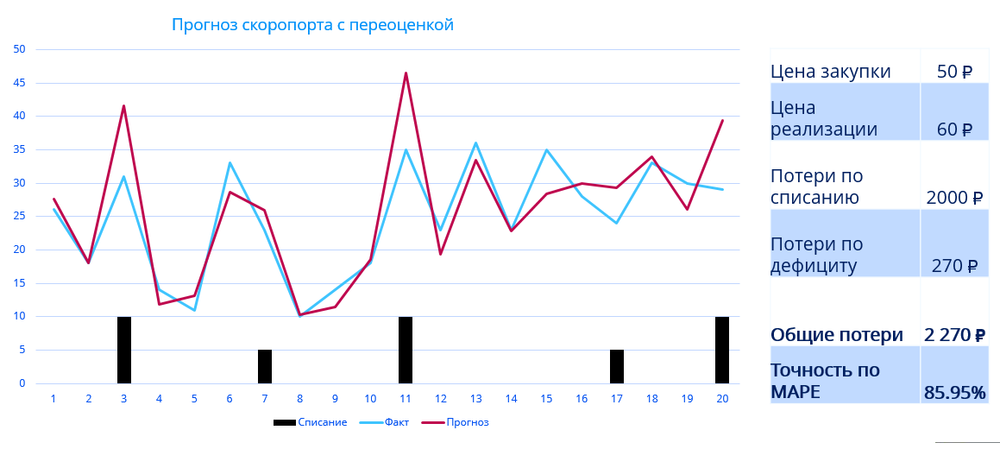
Мы видим достаточно неплохую точность прогнозирования – 85,95%. Черные столбцы – это количество продукции, которую мы перепрогнозированили, и её пришлось списать. Общие потери компании – 2270 рублей.

А теперь посмотрим тот же самый товар, но прогноз другой. В этот раз он постоянно недооценивает продажи.

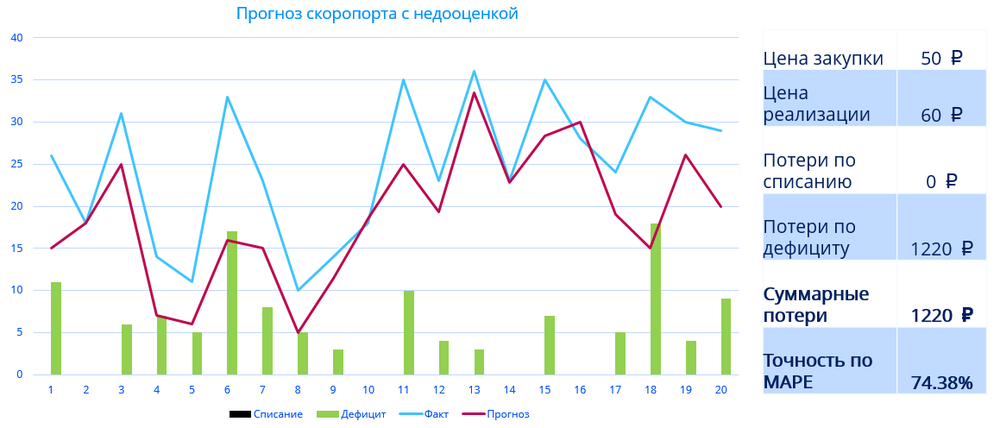
Точность прогнозирования здесь значительно ниже – 74,38%. И при выборе мы должны были остановиться на первом прогнозе, так как там точность значительно выше. Но во втором случае суммарные потери компании снизились практически в 2 раза – до 1220 рублей. И при такой цене закупки, цене реализации и динамике спроса компании будет выгоднее недооценивать спрос, чем переоценивать.

Это показывает, что метрика, выраженная в процентах, не всегда отражает экономическую эффективность. Соответственно, мы можем рассчитывать два различных значения. Если прогноз окажется меньше реального спроса, то он приведет к дефициту, экономический урон от которого рассчитывается по формуле:

Экономический урон = количество недопроданных товаров* (цена реализации - цена закупки)

Например, вы покупаете колесные диски по 3000 рублей за штуку и продаете по 4000. Прогноз на месяц составил 1000 дисков, реальный спрос оказался 1200 штук. В этом случае:

Экономический урон = (1200-1000)*(4000-3000)=200 000 рублей.

В случае превышения прогноза над реальным спросом компания понесет убытки по хранению продукции. В этом случае экономический урон будет рассчитываться так:

Экономический урон = затраты на нереализованную продукцию * ставка альтернативных вложений

Предположим, что реальный спрос в предыдущем примере оказался 800 дисков, и вам пришлось хранить диски еще один месяц. Пусть ставка альтернативных вложений составляет 20% в год. Тогда: 

Экономический урон = (1000-800)*3000*0,2/12=10 000 рублей.

Соответственно, в каждом конкретном случае мы будет учитывать одно из этих значений.

Решение 4. Считать ошибку прогнозирования в деньгах

Проблема 5. Оценивается только точность оперативного прогноза. Страховой запас при этом может достигать до 70% от общего объема запасов

Описанные ошибки распространяются только на прогноз спроса и не описывают страховой запас. А он в некоторых случаях может составлять от 20% до 70% от общих товарных запасов на складе. Поэтому, какой бы точный ни был прогноз с точки зрения описанных выше методов, оценка точности страхового запаса остается за бортом. А значит реальные данные могут быть значительно искажены. Поэтому, даже имея высокую точность прогноза, компания может нести большие потери и быть неэффективной.

Страховой запас может при этом рассчитываться по-разному:

• Интуитивно сотрудниками компании
• Процент от среднедневных продаж
• Используя нормальное распределение для спроса, ошибок прогнозирования или сроков поставки по заданному уровню сервиса I рода

Полезный материал
Руководство по сокращению страхового запаса

Чтобы решить эту проблему, мы предлагаем сравнивать алгоритмы с использованием понятия уровень сервиса. Уровень сервиса (здесь и далее – уровень сервиса II рода, fill rate) – это доля спроса, которую мы гарантировано покроем с использованием имеющихся на складе запасов в течение периода их пополнения. 

Например, уровень сервиса 90% означает, что мы удовлетворим 90% спроса. На первый взгляд может показаться логичным, что уровень сервиса всегда должен составлять 100%. Тогда и прибыль будет максимальна. Но в реальных ситуациях зачастую дело обстоит иначе: удовлетворение 100% уровня сервиса приводит к сильному перезатариванию склада, а для товаров с ограниченными сроками годности – еще и к списанию. И убытки от затрат на хранение, списания просроченной продукции и недополученной прибыли от вложения свободных денег в итоге снизят прибыль от реализации, в случае, если бы мы поддерживали уровень сервиса 95%. Нужно заметить, что для каждой отдельной позиции товаров будет свой оптимальный уровень сервиса.

Подробнее об уровне сервиса, его видах и примерах расчета читайте в статье «Что такое уровень сервиса и почему он важен».

Так как страховой запас может составлять значительную долю, его нельзя игнорировать при сравнении алгоритмов (как это делается при расчете ошибок MAPE, RMSE и т. д.). Поэтому мы делаем сравнение не прогноза, а оптимального запаса с заданным уровнем сервиса. Оптимальный запас для заданного уровня сервиса – это такое количество товаров, которое нужно хранить на складе, чтобы получить максимум прибыли от реализации товаров и одновременно сократить издержки на хранение до минимума.

В качестве основного критерия качества прогнозирования мы используем суммарное значение потерь для заданного уровня сервиса, о котором писали выше. Таким образом, мы оцениваем потери в денежном выражении при использовании данного конкретного алгоритма. Чем меньше потери, тем точнее работает алгоритм.

Здесь нужно заметить, что для разных уровней сервиса оптимальный запас тоже может различаться. И в одном случае прогноз будет точно в него попадать, а в другом возможны перекосы в большую либо меньшую сторону. Так как многие компании не рассчитывают оптимальный уровень сервиса, а используют заданный заранее, значение основного критерия мы вычисляем для всех самых распространенных уровней сервиса: 70%, 75%, 80%, 85%, 90%, 95%, 98%, 99% и суммируем потери. Таким образом, мы можем проверить, насколько хорошо в целом работает модель.

Давайте рассмотрим пример. Возьмем несколько методов. Для каждого из них мы можем оценить, какие запасы он нам предложит на разных уровнях сервиса. Используя исторические данные за прошедшие полгода, можно посчитать, к чему бы это привело: сколько фактического спроса было бы удовлетворено, сколько запасов бы лежало на складе, сколько товаров пришлось бы списать и т. д. Все эти суммарные потери мы можем представить одной цифрой. 

В примере самым неэффективным будет метод №4, а самым эффективным – метод № 2

Решение 5. Планировать товарные запасы в соответствии с заданным уровнем сервиса II рода

Как можно еще улучшить модель?

Использование фиксированного уровня сервиса – это уже устаревший метод. Современные программные продукты позволяют динамически управлять уровнем сервиса для каждой товарной позиции. Человеку нет необходимости делать это самостоятельно, экспертным путем. Программа сама определит, что выгоднее – держать на складе несколько лишних десятков товаров или, наоборот, поддерживать дефицит. Уровень сервиса для конкретного SKU будет рассчитан автоматически с учетом всевозможных рисков. Это называется оптимальный уровень сервиса.

Такой подход заставляет нас считать ошибку прогнозирования совсем по-другому. Экономический урон в этом случае будет выглядеть как соотношение потерь на оптимальном уровне сервиса по ожидаемому (модельному) распределению продаж и по реальному распределению продаж (по факту). 

Прогнозируемое значение оптимального уровня сервиса не всегда соответствует оптимальному значению уже на реальном распределении продаж. Поэтому мы должны сравнивать ошибку между прогнозом объема продаж на оптимальном (по модели) уровне сервиса и реальным объемом продаж, обеспечивающим оптимальное значение уровня сервиса по реальным данным. 

Проиллюстрируем это на прошлом примере с дисками. Предположим, что прогнозное значение оптимального уровня сервиса для него составляет 90%, а оптимальный объем запаса для этого случая примем равным 3000 колесных дисков. Пусть в первом случае реальный уровень сервиса оказался выше прогнозного и составил 92%. Соответственно объем заказов также вырос и составил 3300 дисков. Ошибка прогнозирования будет рассчитываться как разность между реальным и фактическим объемом продаж, умноженная на разность цен реализации. Итого, мы имеем:

(3300-3000)*(4000-3000)=300 000 рублей.

Теперь представим обратную ситуацию: реальный уровень сервиса оказался меньше прогнозного и составил 87%. Реальный объем продаж при этом составил 2850 дисков. Ошибка прогнозирования будет рассчитана, как сумма затрат на нереализованную продукцию, умноженную на ставку альтернативных вложений за этот период (в качестве примера берем период сроком месяц и ставку, равную 20% годовых). Итоговое значение критерия будет равно:

(3000-2850)*3000*0,2/12 = 7500 рублей

Используемые критерии, в отличие от классических математических ошибок, показывают суммарные потери в деньгах при применении той или иной модели. Так как оптимальный уровень сервиса может меняться, то мы комбинируем подходы – расчет потерь на оптимальном уровне сервиса и суммарные значения потерь на распространенных уровнях сервиса. Соответственно, наилучшей будет модель, которая обеспечивает минимальные потери. Такой подход позволяет бизнес-пользователям оценить работу различных алгоритмов на понятном им языке.  

Пример сравнения 4-х методов по 2 критериям. Чем меньше потери, тем эффективнее метод.

 

Практические рекомендации
по управлению запасами
Про прогнозирование спроса, управление ассортиментом, планирование запасов, автоматизацию расчетов и сокращение стоков

Подписаться на телеграм канал