Авторегрессия (AR, autoregression)

Обновление статьи от 04.07.2019г.

В статье приводится сравнение алгоритмов прогнозирования для решения задачи управления товарными запасами с использованием ошибки прогнозирования RMSE. На текущий момент мы не рекомендуем пользоваться этим методом. О причинах отказа от сравнения с использованием ошибок прогнозирования, читайте в статье Почему мы не считаем MAPE, RMSE и другие математические ошибки при прогнозировании спроса Рекомендуемый способ сравнения – имитационное моделирование.

Метод Авторегрессии (AR, autoregression) относится к алгоритмам прогнозирования 1 поколения (либо 2-го поколения при наличии страхового запаса по модельному распределению спроса). Он подходит только для прогнозирования товаров с гладким регулярным спросом, который характерен приблизительно 6% ассортимента типового продуктового супермаркета и не характерен практически ни для каких товаров других отраслей. Поэтому мы рекомендуем прогнозировать товарные запасы, а не спрос.

Подробнее о поколениях алгоритмов прогнозирования в видео "Эволюция алгоритмов прогнозирования спроса"

Также рекомендуем прочитать статью "Почему нужно прогнозировать товарные запасы, а не спрос?"

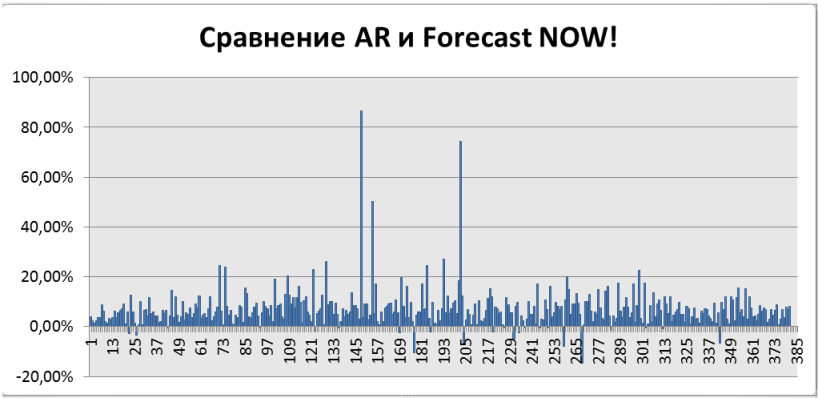
Результаты сравнения обобщены на графике ниже, по оси Х – товары, по оси Y – на сколько процентов Forecast NOW! оказывается лучше, чем алгоритм авторегрессии. Как можно видеть, почти всегда, алгоритм Forecast NOW! прогнозирует точнее на 10-20%. Подробнее об алгоритме и сравнении читайте ниже.

Общее описание модели авторегрессии

 Прогнозирование с использованием модели авторегрессии опирается на предыдущие значения продаж. Слово авторегрессия означает зависимость последующего значения продажи от предыдущих продаж. Зависимость в случае авторегрессии предполагается линейная, то есть прогноз представляет собой сумму продаж за предыдущие дни с некоторыми коэффициентами, которые являются постоянными и определяют параметры модели авторегрессии. Сколько дней (периодов в общем случае) таких продаж из прошлого мы будем брать, чтобы пытаться спрогнозировать будущие продажи называется порядком модели авторегрессии p. Например, хотим на вход давать продажи за предыдущие три дня, а прогнозировать, сколько будет продано в следующий день. Тогда, порядок модели p = 3. Кратко это часто записывается как AR(3). Формула будет иметь вид 

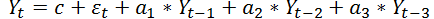
Здесь еще имеются непонятные буквы. Во-первых, это c – это постоянная величина, которая всегда прибавляется к прогнозу и набор коэффициентов 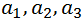  на которые умножаются наши продажи в прошлые периоды. Также имеется  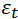. Не вдаваясь в детали,  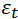 – это белый шум, случайная компонента. Это тоже последовательность чисел, также как и продажи. И для прогнозирования на 10ый день, в формулу подставляется значение вот этого ряда, белого шума в 10-ый «день» (период). Вот как выглядит на картинке белый шум  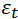 (Рисунок 1)

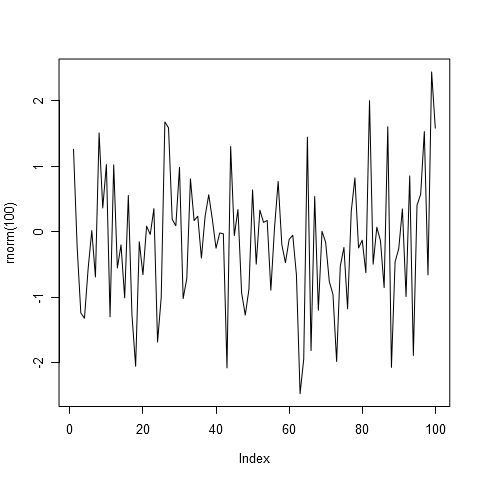
Рисунок 1а. Белый шум в авторегрессии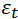

В спросе присутствует случайная составляющая, так вот это слагаемое его моделирует. Для того чтобы пользоваться всем этим необходимо выбрать все перечисленные параметры. Конечно, для этого существуют специальные программы, которые определяет оптимальные значения параметров авторегрессии. Конечный пользователь просто может воспользоваться готовой моделью и получить прогноз. 

На плечи пользователя ложится ответственность за выбор порядка модели авторегрессии. Сколько и какие дни включать в модель. Для прогнозирования на завтра учитывать продажи за каждый день предыдущей недели или только за несколько, а может лучше учитывать продажи ровно неделю назад? Вот здесь возможно несколько подходов. Полный перебор всех моделей в надежде найти хорошую модель или проанализировать ряды, применить хитрые статистические приемы и понять какие продажи больше всего влияют на то, что будет продано в следующем периоде. 

Можно ли учитывать сезонность в модели авторегрессии? Оказывается, что можно. Для этого необходимо добавить в модель продажи за прошлый сезон. Например, если сезонность недельная, то мы добавим продажи за 7 дней назад. Если годовая сезонность, а мы прогнозируем по месяцам, то в модель авторегрессии мы включим продажи за месяц год назад.

Давайте посмотрим, как выглядит в общем виде модель авторегрессии.

 Пусть наши продажи это Y. Тогда продажи в первый день это 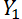, продажи во второй день  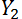и так далее. Пусть мы хотим узнать прогноз 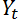на день t. На языке формул это выглядит следующим образом 

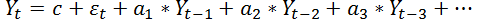
Теперь давайте посмотрим, как данный метод работает в реальных условиях.  Весь процесс начинается с «подгонки» выбранной модели, а именно ее порядка, к исходным данным. Казалось бы, чем точнее мы подгоним модель к исходным данным, тем лучше должен быть прогноз. На самом деле, это не так. Исходные данные содержат много шума, провалов, выбросов. Если все это попадет в модель (а при большом порядке именно так и будет), то авторегрессия в качестве прогноза ничего хорошего не выдаст. Она не сможет обобщить имеющиеся тенденции, а просто запомнит те данные, что были со всеми их недостатками. И спрогнозирует не спрос, а проблемы со складом и резкие выбросы. 

Как же определить ту грань, когда стоит прекратить увеличивать порядок авторегрессии и включать все больше дней в модель прогнозирования? Для этого существует множество разных методик. Например, вводится штраф за сложность модели. Но тут тоже таится трудность, какой назначить штраф? Что лучше авторегрессия с двумя параметрами и точностью 75% или авторегрессия с тремя параметрами и точностью 92%. Различных видов штрафа тоже очень много, они активно исследуются, но это уже другая история.

Как прогнозирующий метод ведет себя на исторических, известных ему данных называется моделью. Давайте сначала посмотрим на модели, построенные при различных порядках авторегрессии.

Модели авторегресии

  На рисунке 1а и всех последующих реальные данные о продажах представлены, синим цветом. По оси X откладывается номер периода (в данном случае день), а по оси Y–объем продажи. 

Рисунок 1б. Авторегрессия, порядок модели  p = 1 

 

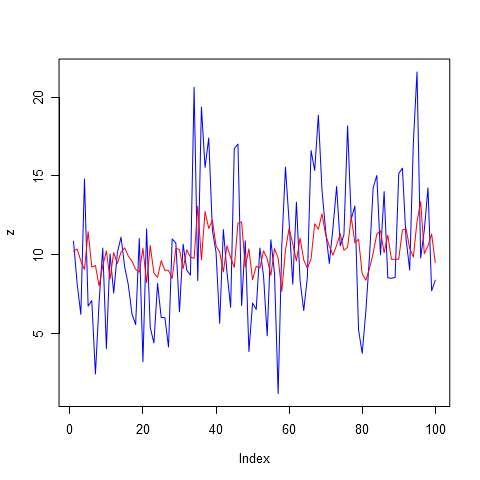
Как можно видеть из рисунка 1б и 2 низкий порядок авторегрессии обеспечивает приближение только к самым незначительным пикам. Очевидно, будущие продажи определяются не только тем, что было продано вчера и позавчера.

Рисунок 2. Авторегрессия, порядок модели  p = 2

 

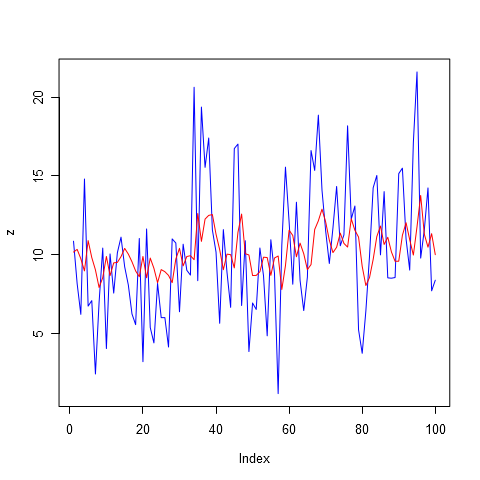
Давайте увеличим порядок авторегрессии до восьми в надежде учесть недельную сезонность продаж. Обратите внимание на график, представленный на рисунке 3. Модель стала гораздо более точной. Но значит ли, что она даст самый лучший прогноз? К сожалению, ответ здесь не очевиден. 

Рисунок 3. Авторегрессия, порядок модели  p = 8

 

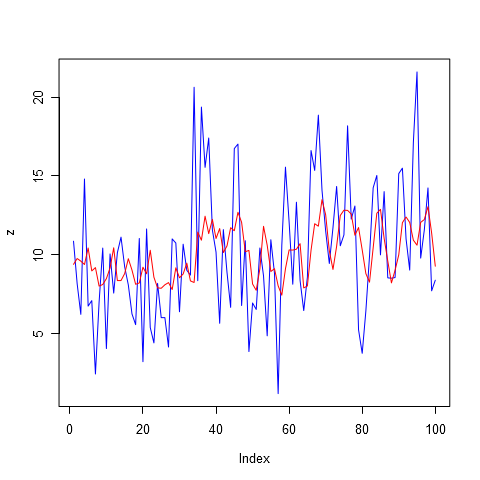
Теперь давайте увеличим показатель авторегрессии до 14, здесь уже может быть учтена двухнедельная сезонность, а также все 14 дней прошлых продаж. Ведь мы не ограничивали модель на то, чтобы какие-то дни из этих 14 не учитывались.  Так что в ходе подстройки модели под исторические данные она сама решила, продажам каких дней назначить коэффициент больше, а каким меньше. Вместе с увеличением числа учитываемых дней, мы, конечно же, увеличиваем и число шума, которое закладываем в наш будущий прогноз. Авторегрессия порядка 14 представлена на рисунке 4.

Рисунок 4. Авторегрессия, порядок модели  p = 14

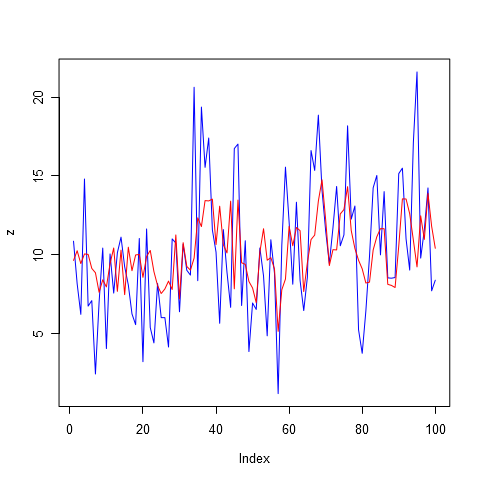
Ну и для завершения картины, чтобы иметь представление как замечательно выглядит модель при порядке авторегрессии равным 28, посмотрите на рисунок 5. Все пики почти в точности повторяются моделью. Но, еще раз повторюсь, это не означает, что данная модель даст нам отличный прогноз. Использование штрафов, скорее всего, не пропустило бы данную модель даже в тройку лидеров.

 Рисунок 5. Авторегрессия, порядок модели  p = 28

Прогнозы

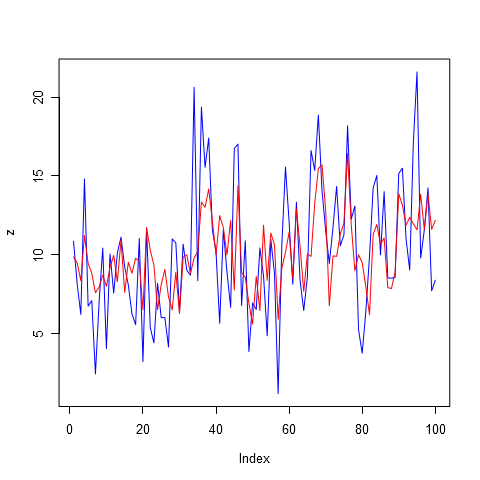
Давайте теперь посмотрим на прогнозы, которые были получены с использованием различных моделей авторегрессии с разным порядком. На рисунке 6 представлена модель авторегрессии первого порядка. Очевидно, прогнозировать продажи по одному прошлому периоду для этого товара нелогично.  Но можно заметить, что система некоторые спады и подъемы успешно спрогнозировала, не смотря на то, что амплитуды не хватило. Прогноз очень похож на среднее, но это не значит, что этот вариант самый худший. Может быть продажи настолько хаотичны, что другие модели покажут результат хуже.

 Рисунок 6. Прогноз на 56 дней вперед, авторегрессия порядка 1, AR(1)

 

Прогноз с использованием 4 прошлых значений уже больше отличается от простого среднего. Он представлен на рисунке 7.

 Рисунок 7. Прогноз на 56 дней вперед, авторегрессия порядка 4, AR(4)

 

На рисунке 8 можно заметить, что система становится более изменчивой. Все больше появляется пиков и провалов в прогнозе. Если посчитать ошибки по всем прогнозам, то можно заметить, что это самый лучший прогноз. Имеет ошибку 6.96. Оно и не удивительно, учитывая недельную сезонность данного товара, нам удается получить большую часть информации и минимизировать шум.

Рисунок 8. Прогноз на 56 дней вперед, авторегрессия порядка 8, AR(8)

 

На рисунках 9 и 10 представлены примеры прогнозов для моделей авторегрессии с большими значениями порядка 14 и 32. Ошибки для них соответственно составляют 7.03 и 7.45. Увеличение порядка начинает отрицательно сказываться на качестве прогноза.

 Рисунок 9. Прогноз на 56 дней вперед, авторегрессия порядка 14, AR(14)

 

 Рисунок 10. Прогноз на 56 дней вперед, авторегрессия порядка 32, AR(32)

 

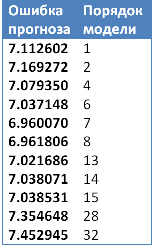
В заключение наглядного обзора алгоритма прогнозирования на основе авторегрессии приведем сводную таблицу по ошибкам прогнозирования для рассмотренного примера. Минимум как мы можем видеть из таблицы 2, достигается при порядке модели, равным 7ми.
 

 

Таблица 1. Ошибки прогнозирования авторегрессии при различных порядках модели

Сравнение

Ошибки прогнозирования авторегрессии при различных порядках модели. Для сравнения с алгоритмом ForecastNOW! были построены прогнозы методом авторегрессии с различными параметрами, выбиралась лучшая модель, исходя из ошибки на известных данных (модели) с учетом модели штрафов за сложность системы. Для выбора оптимальных параметров была написана программа на языкепрограммирования R. Ошибки прогнозирования (RMSE) представлены в таблице 3.

На рисунке 11 представлен график сравнения ForecastNOW! и авторегрессии (AR). По оси Х отложены товары, по оси Y на сколько алгоритм ForecastNOW! лучше или хуже алгоритма авторегрессии в процентах. Положительный процент показывает, что ForecastNOW! лучше на обозначенное число процентов, отрицательный – хуже. Как можно видеть из графика почти во всех случаях алгоритм ForecastNOW! оказывается значительно лучше (в среднем на 10-20%), то есть предоставляет более точный прогноз. А более точный прогноз в свою очередь позволяет точнее планировать необходимые товарные запасы.

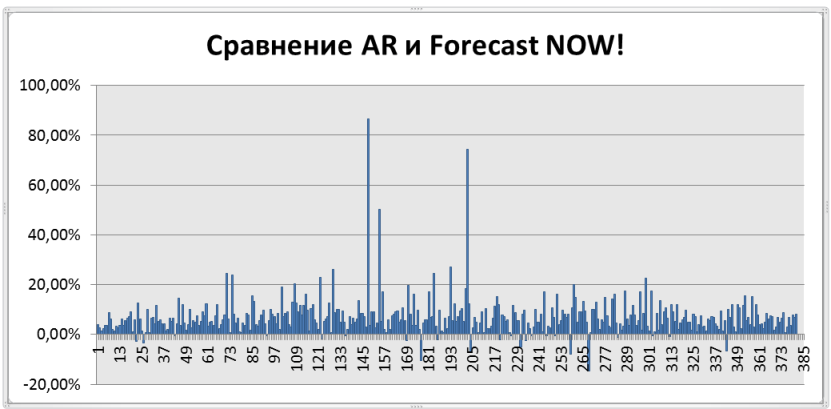
 Рисунок 11. Сравнение точности прогнозирования авторегрессии и алгоритма ForecastNOW!

 

 

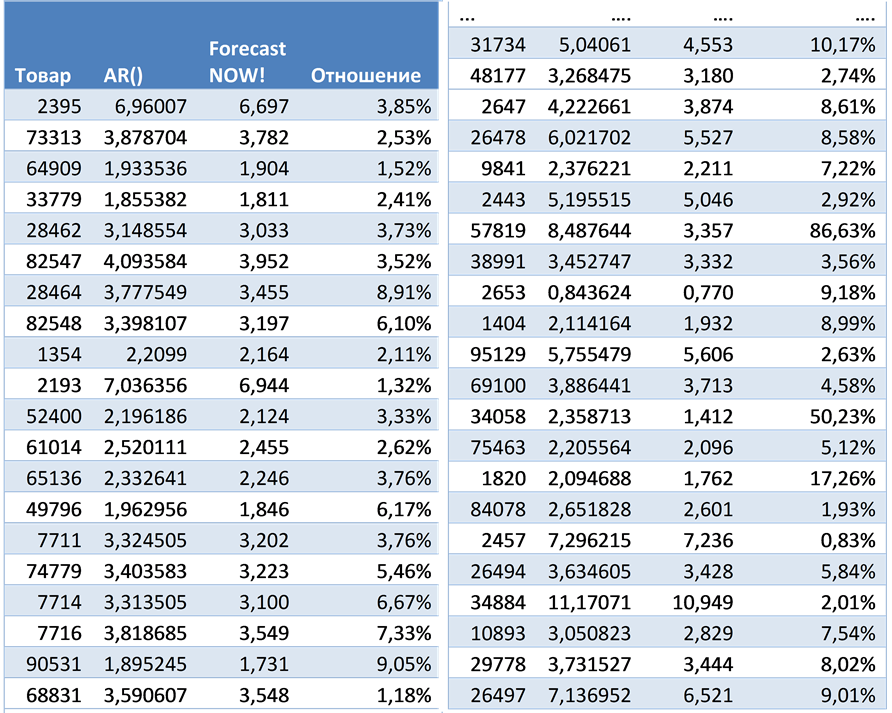
Таблица 2. Ошибки прогнозирования авторегрессии и алгоритма ForecastNOW!, а также процентное соотношение качества прогнозов

Обзор других методов:

• Экспоненциальное сглаживание (1-2 поколение);
• Простая скользящая средняя (SMA, Simple Moving Average) (1-2 поколение);
• Метод Хольта-Винтерса (1-2 поколение);
• Вероятностное прогнозирование (4 поколение)