Обновление статьи от 04.07.2019г.
В статье приводится сравнение алгоритмов прогнозирования для решения задачи управления товарными запасами с использованием ошибки прогнозирования RMSE. На текущий момент мы не рекомендуем пользоваться этим методом. О причинах отказа от сравнения с использованием ошибок прогнозирования, читайте в статье Почему мы не считаем MAPE, RMSE и другие математические ошибки при прогнозировании спроса Рекомендуемый способ сравнения – имитационное моделирование.
Метод Простой скользящей средней (SMA,Simple Moving Average) относится к алгоритмам прогнозирования 1 поколения (либо 2-го поколения при наличии страхового запаса по модельному распределению спроса). Он подходит только для прогнозирования товаров с гладким регулярным спросом, который характерен приблизительно 6% ассортимента типового продуктового супермаркета и не характерен практически ни для каких товаров других отраслей. Поэтому мы рекомендуем прогнозировать товарные запасы, а не спрос.
Подробнее о поколениях алгоритмов прогнозирования в видео "Эволюция алгоритмов прогнозирования спроса"
Также рекомендуем прочитать статью "Почему нужно прогнозировать товарные запасы, а не спрос?"
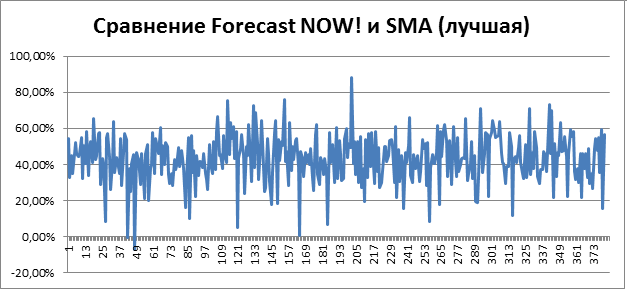
Сравнение Forecast NOW! и модели Простой скользящей средней (SMA, Simple Moving Average) вы можете увидеть на графике ниже. По оси X - номер товара, по оси Y - процентное улучшение качества прогноза. Описание модели, детальное исследование, результаты экспериментов читайте ниже.
Описание модели
Суть алгоритма прогнозирования заключается в усреднении значений продаж за определенный период, называемый окном T. Идея алгоритма заключается в том, что в будущем будет продано столько, сколько в среднем было продано в прошлом. Ширина окна T определяет, сколько прошлых периодов будут учитываться при прогнозировании.
Чем больше мы возьмем T, тем более гладким и плавным получится наш прогноз. Если мы возьмем ширину окна T равной всему промежутку продаж товара, то прогноз будет соответствовать среднему за весь период. Уменьшая размер окна, мы можем контролировать «память» прогнозирующей модели.
Если говорить на языке формул, то скользящая средняя равна среднему арифметическому значений продаж за установленный период и вычисляется следующим образом:
Y(t+1)=(1/(T+1))*[C(t)+C(t-1)+...+C(t-T)]
- Где Y(t+1) – прогноз на t+1 период,
- T – число прошлых периодов, которые мы рассматриваем при усреднении,
- C – реальные продажи, C(t) – продажи в день t
Как можно заметить, параметром данной модели прогнозирования является ширина окна T. Чтобы получить хороший прогноз, нужно выбрать оптимальное значение этого параметра. Сложность заключается в том, что заранее неизвестно каким окажется прогноз (хорошим или плохим) при различных значениях этого параметра.
Для примера, давайте посмотрим на продажи товара X, и его скользящие средние, построенные для различных значений скользящего окна T. Графики для T={3, 4, 6} приведены на рисунках 1, 2, 3 соответственно.
На рисунке 1 изображен прогноз скользящей средней на один шаг вперед, в качестве прогноза принимается среднее за предыдущие 3 недели (так как T = 3)
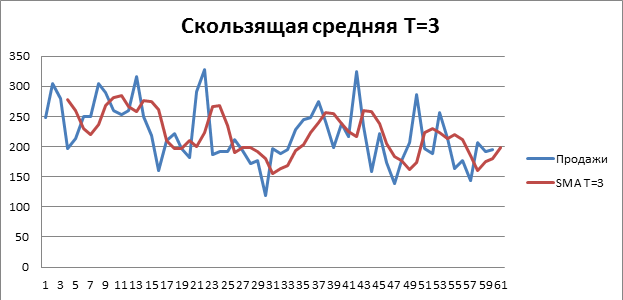
Рисунок 1. Скользящая средняя при T = 3
На рисунке 2 изображен прогноз скользящей средней на один шаг вперед, в качестве прогноза принимается среднее за предыдущие 4 недели (так как T = 4). Как можно заметить прогноз становится более гладким.
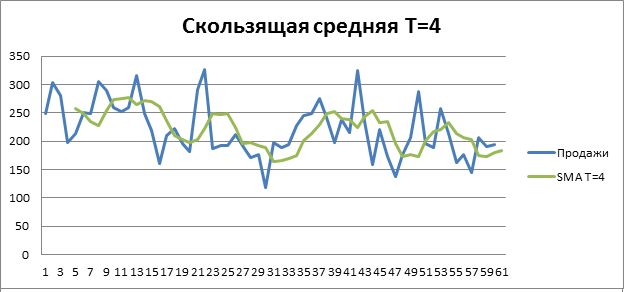
Рисунок 2. Скользящая средняя при T = 4
На рисунке 3 изображен прогноз скользящей средней на один шаг вперед, в качестве прогноза принимается среднее за предыдущие 6 недель (так как T = 6). Можно заметить, что график прогноза стал еще больше похожим на простое среднее.
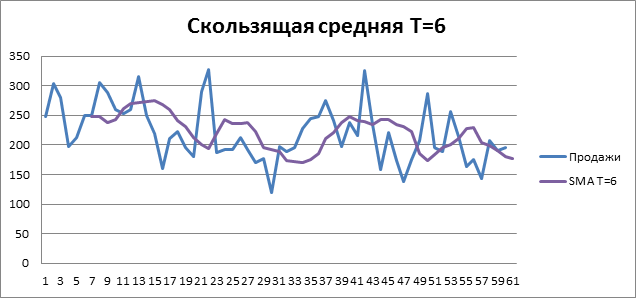
Рисунок 3. Скользящая средняя при T = 6
Определить параметр T можно эмпирически, на основе качества прогнозов предыдущих периодов. Так для рассмотренных примеров ошибки прогнозов следующие
|
Ошибка |
SMA T=3 |
SMA T=4 |
SMA T=6 |
|
RMSE |
48,874388 |
48,205074 |
52,293842 |
Исходя из этой таблицы, предпочтительным оказывается алгоритм простой скользящей средней со сглаживающим окном шириной 4. Конечно, мы не рассмотрели всевозможные варианты, возможно, есть и более качественные модели.
Сравнение модели Простой скользящей средней с Forecast NOW!
Для сравнения с алгоритмом Forecast NOW! были построены прогнозы методами скользящей средней для разной ширины окна от 2 до 8, выбирался лучший прогноз (хотя на самом деле в реальной ситуации сделать этого нельзя). Ошибки прогнозирования (RMSE) представлены в таблице 1.
На рисунке 4 представлен график сравнения Forecast NOW! и простой скользящей средней (заведомо лучшая модель, что недостижимо при реальном ее использовании). По оси Х отложены товары, по оси Y на сколько алгоритм Forecast NOW! лучше или хуже алгоритма простой скользящей средней в процентах. Положительный процент показывает, что Forecast NOW! лучше на обозначенное число процентов, отрицательный – хуже. Как можно видеть из графика почти во всех случаях алгоритм Forecast NOW! оказывается значительно лучше (в среднем на 40%), то есть предоставляет более точный прогноз в ~1.5 раза.

Рисунок 4. Сравнение алгоритма Forecast NOW! и простой скользящей средней
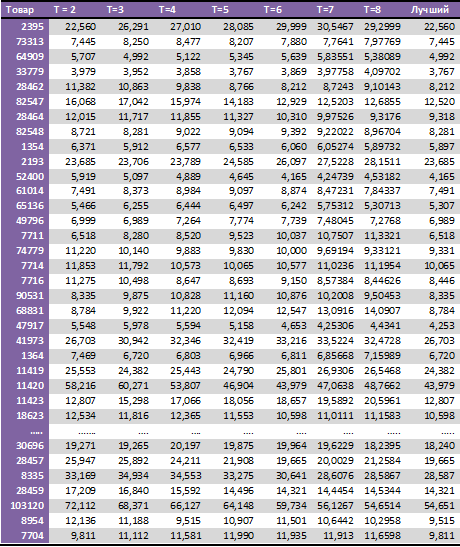
Таблица 1. Ошибки прогнозирования для различных моделей скользящего среднего с шириной окна от 2 до 8 (сокращенная)
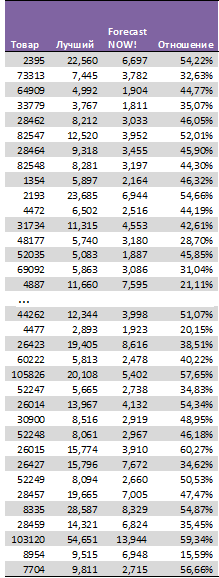
Таблица 2. Сравнение прогнозов модели скользящего среднего и Forecast NOW!
Обзор других методов:
- Экспоненциальное сглаживание (1-2 поколение);
- Авторегрессия (1-2 поколение);
- Метод Хольта-Винтерса (1-2 поколение);
- Вероятностное прогнозирование (4 поколение)