Обновление статьи от 04.07.2019г.
В статье приводится сравнение алгоритмов прогнозирования для решения задачи управления товарными запасами с использованием ошибки прогнозирования RMSE. На текущий момент мы не рекомендуем пользоваться этим методом. О причинах отказа от сравнения с использованием ошибок прогнозирования, читайте в статье Почему мы не считаем MAPE, RMSE и другие математические ошибки при прогнозировании спроса Рекомендуемый способ сравнения – имитационное моделирование.
Метод Экспоненциального сглаживания относится к алгоритмам прогнозирования 1 поколения (либо 2-го поколения при наличии страхового запаса по модельному распределению спроса). Он подходит только для прогнозирования товаров с гладким регулярным спросом, который характерен приблизительно 6% ассортимента типового продуктового супермаркета и не характерен практически ни для каких товаров других отраслей. Поэтому мы рекомендуем прогнозировать товарные запасы, а не спрос.
Подробнее о поколениях алгоритмов прогнозирования в видео "Эволюция алгоритмов прогнозирования спроса"
Также рекомендуем прочитать статью "Почему нужно прогнозировать товарные запасы, а не спрос?"
Насколько Forecast NOW! лучше модели Экспоненциального сглаживания (ES) вы можете увидеть на графике ниже. По оси X - номер товара, по оси Y - процентное улучшение качества прогноза. Описание модели, детальное исследование, результаты экспериментов читайте ниже.
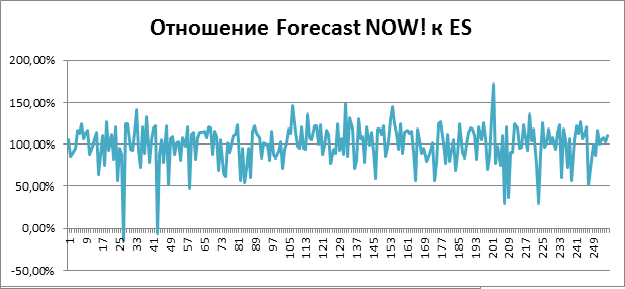
Описание модели
Прогнозирование методом экспоненциального сглаживания является одним из самых простых способов прогнозирования. Прогноз может быть получен только на один период вперед. Если прогнозирование ведется в разрезе дней, то только на один день вперед, если недель, то на одну неделю.
Для сравнения прогнозирование проводилось на неделю вперед в течение 8 недель.
Что такое экспоненциально сглаживание?
Пусть ряд С представляет исходный ряд продаж для прогнозирования
С(1)– продажи в первую неделю, С(2) во второй и так далее.
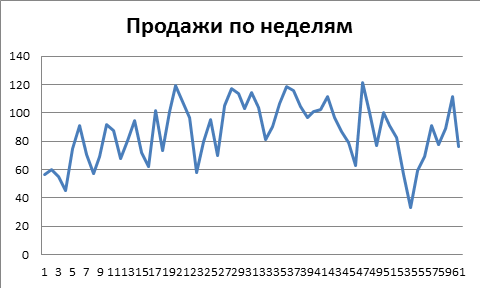
Рисунок 1. Продажи по неделям, ряд С
Аналогично, ряд S представляет собой экспоненциально сглаженный ряд продаж. Коэффициент α находится от нуля до единицы. Получается он следующим образом, здесь t – момент времени (день, неделя)
S (t+1) = S(t) + α *(С(t) – S(t))
Большие значения константы сглаживания α ускоряют отклик прогноза на скачок наблюдаемого процесса, но могут привести к непредсказуемым выбросам, потому что сглаживание будет почти отсутствовать.
Первый раз после начала наблюдений, располагая лишь одним результатом наблюдений С (1), когда прогноза S(1) нет и формулой (1) воспользоваться еще невозможно, в качестве прогноза S(2) следует взять С (1).
Формула легко может быть переписана в ином виде:
S(t+1) = (1 – α)* S(t) + α * С(t).
Таким образом, с увеличением константы сглаживания доля последних продаж увеличивается, а доля сглаженных предыдущих уменьшается.
Константа α выбирается опытным путем. Обычно строится несколько прогнозов для разных констант и выбирается наиболее оптимальная константа с точки зрения выбранного критерия.
Критерием может выступать точность прогнозирования на предыдущие периоды.
В своем исследовании мы рассмотрели модели экспоненциального сглаживания, в которых α принимает значения {0.2, 0.4, 0.6, 0.8}. Для сравнения с алгоритмом прогнозирования Forecast NOW! для каждого товара строились прогнозы при каждом α, выбирался наиболее точный прогноз. В действительности же, ситуация обстояла бы гораздо более сложная, пользователю не зная наперед точности прогноза нужно определиться с коэффициентом α, от которого очень сильно зависит качество прогноза. Вот такой замкнутый круг.
Наглядно
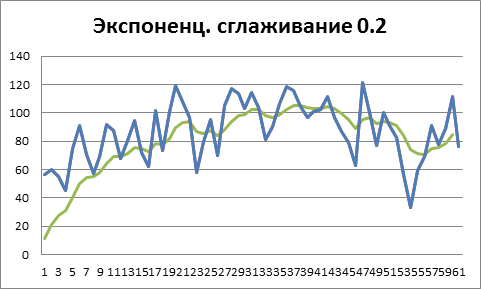
Рисунок 2. α =0.2 , степень экспоненциального сглаживания высокая, реальные продажи учитываются слабо
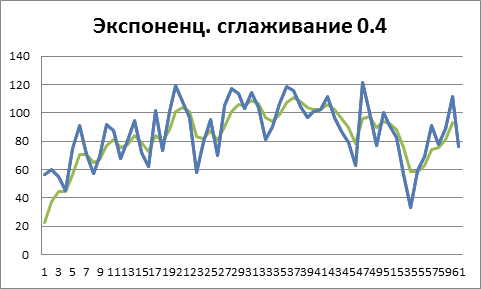
Рисунок 3. α =0.4 , степень экспоненциального сглаживания средняя, реальные продажи учитываются в средней степени
Можно видеть как с увеличением константы α сглаженный ряд все сильнее соответствует реальным продажам, и если там присутствуют выбросы или аномалии, мы получим крайне неточный прогноз.
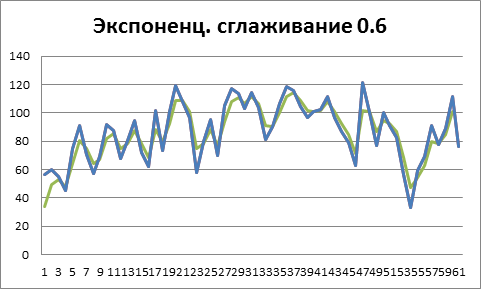
Рисунок 4. α =0.6 , степень экспоненциального сглаживания низкая, реальные продажи учитываются значительно
Можем видеть, что при α=0.8 ряд почти в точности повторяет исходный, а значит прогноз стремится к правилу «будет продано столько же, сколько и вчера»
Стоит отметить, что здесь совершенно нельзя ориентироваться на ошибку приближения к исходным данным. Можно добиться идеального соответствия, но получить неприемлемый прогноз.
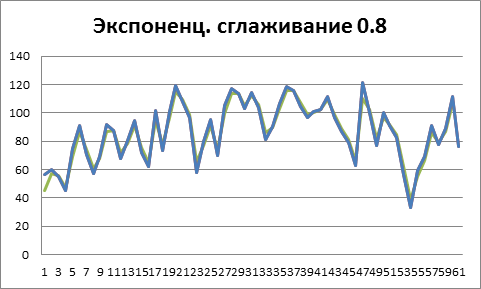
Рисунок 5. α =0.8 , степень экспоненциального сглаживания крайне низкая, реальные продажи учитываются сильно
Примеры прогнозов
Теперь давайте посмотрим на прогнозы, которые получаются с использованием различных значений α. Как можно видеть из рисунка 6 и 7, чем больше коэффициент сглаживания, тем точнее повторяет реальные продажи с опозданием на один шаг, прогноз. Такое опоздание на деле может оказаться критичным, поэтому нельзя просто выбирать максимальное значение α. Иначе получится ситуация, когда мы говорим, что будет продано ровно столько, сколько было продано в прошлый период.
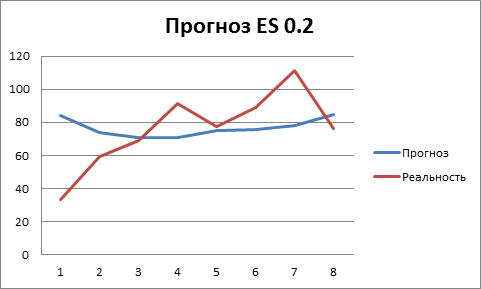
Рисунок 6. Прогноз метода экспоненциального сглаживания при α=0.2
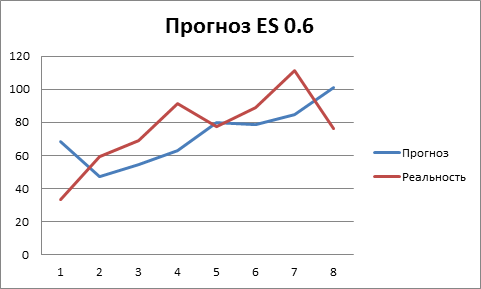
Рисунок 7. Прогноз метода экспоненциального сглаживания при α=0.6
Давайте посмотрим, что получается при α = 1.0. Напомним, S – прогнозируемые (сглаженные) продажи, C – реальные продажи.
S(t+1) = (1 – α)* S(t) + α * С(t).
S(t+1) = С(t).
Продажи в t+1 день согласно прогнозу равны продажам в предыдущий день. Поэтому к выбору константы надо подходить с умом.
Сравнение с Forecast NOW!
Теперь рассмотрим данный метод прогнозирования в сравнении с Forecast NOW!. Сравнение велось на 256 товарах, которые имеют различные продажи, с сезонностью краткосрочной и долгосрочной, с «плохими» продажами и дефицитом, акциями и прочими выбросами. Для каждого товара был построен прогноз по модели экспоненциального сглаживания, для различных α, выбирался лучший и сравнивался с прогнозом по модели Forecast NOW!
В таблице ниже вы видите значение ошибки прогноза для каждого товара. Ошибка здесь считалась как RMSE. Это корень из среднеквадратичного отклонения прогноза от реальности. Грубо говоря, показывает, на сколько единиц товара мы отклонились в прогнозе. Улучшение показывает, на сколько процентов прогноз Forecast NOW! лучше, если цифра положительная, и хуже, если отрицательная. На рисунке 8 по оси X отложены товары, по оси Y указано насколько прогноз Forecast NOW! лучше, чем прогнозирование методом экспоненциального сглаживания. Как можно видеть из этого графика, точность прогнозирования Forecast NOW! почти всегда в два раза выше и почти никогда не хуже. На деле это означает, что использование Forecast NOW! позволит в два раза сократить запасы или снизить дефицит.

Рисунок 8. Сравнение точности прогнозирования Forecast NOW! и метода экспоненциального сглаживания
Таким образом, можно сделать вывод, что прогнозирование с использованием простой модели экспоненциального сглаживания дает результаты гораздо хуже, нежели Forecast NOW!
Вы можете ознакомиться с результатами прогнозирования по каждому товару. Таблицы приведены в сокращенном варианте, для ознакомления с полным вариантом, напишите нам info@forecastnow.ru, мы вам вышлем подробные результаты.
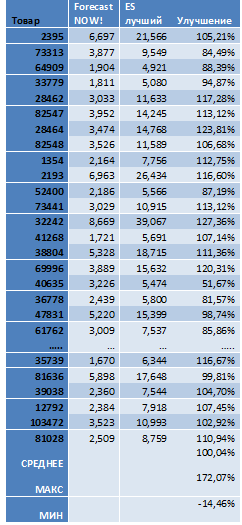
Таблица 1. Сравнение ошибок прогнозирования Forecast NOW! и экспоненциального сглаживания (в сокращении)
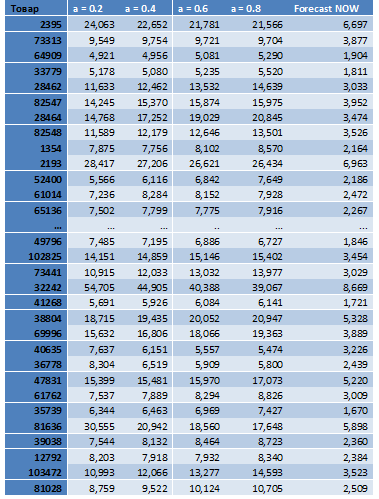
Таблица 2. Ошибки прогнозирования эксп. сглаживания с различными значениями коэффициента α (в сокращении)
Обзор других методов:
- Метод Хольта-Винтерса (1-2 поколение);
- Простая Скользящая средняя (SMA, Simple Moving Average) (1-2 поколение);
- Авторегрессия (1-2 поколение);
- Вероятностное прогнозирование (4 поколение)