Нам часто задают вопрос о работе алгоритмов в Forecast NOW!. Для специалистов важно понимать их принципы и ограничения. От этого зависит эффективность работы сотрудников и прибыль компании.
В статье последовательно разберем, как работает алгоритм подневного вероятностного моделирования с учетом дат поступлений. Покажем на примерах, с какими проблемами сталкивались наши клиенты, и как алгоритмы, заложенные в Forecast NOW!, помогли их решить.
Алгоритмы прогнозирования спроса. Краткий обзор
Прежде чем перейти к описанию моделей, стоит сделать небольшой экскурс на тему развития поколений алгоритмов. По нашим наблюдениям, большинство российских компаний используют методы прогнозирования спроса, которые устарели еще 10-15 лет назад. Это такие методы, как среднедневные продажи, ARIMA, скользящая средняя, экспоненциальное сглаживание, метод Хольта-Уинтерса и другие.
Все эти методы подразумевают, что в результате работы алгоритма мы получим одно число, как прогноз спроса на период. Например, прогноз спроса докторской колбасы на неделю составит 120 шт. Единственное значение на выходе из алгоритма – это один из главных недостатков таких методов. Каким бы точными они не казались – в реальных рыночных условиях это всегда риск. Никто не может точно угадать, какой будет спрос завтра или на следующей неделе. И оценивать его одним числом – значит, заведомо допускать ошибку.
Чтобы снизить риск вышеописанной ошибки, на практике обычно используют страховой запас. В некоторых случаях он может достигать до 70% от общего объема запасов. Недостаток кроется в методе расчета страхового запаса. Обычно предполагается, что распределение товара соответствует Нормальному (либо Пуассоновскому). Но оно подходит только для товаров регулярного спроса. Это, как правило, 4-6% товаров от ассортимента обычного продуктового супермаркета. Для остальных товаров редкого спроса оно мало применимо, что было научно доказано (см. научную справку)
Мы в Forecast NOW! для прогнозирования используем полновероятностные модели. Это последнее поколение алгоритмов прогнозирования спроса на момент написания статьи (сентябрь 2020 года). В отличие от методов, описанных выше, на выходе мы получаем прогноз спроса в виде распределения вероятностей, а не одного числа (подробные описание ниже в статье). Это уже дает возможность компании управлять рисками. Например, зная, что спрос на колбасу докторскую будет равен 120 шт. с 30% вероятностью, можно уже понять, стоит ли заказывать такой объем.
Одно из главных преимуществ вероятностных моделей – они для каждого товара строят собственное распределение объемов спроса, а не используют обобщенные модели. Фактически для каждого SKU используется индивидуальная модель, описывающая изменения спроса, характерные только для этого товара. Поэтому такой подход в реальных рыночных условиях постоянных рисков и неопределенности оказывается лучше.
Подробнее о поколениях алгоритмов прогнозирования и их отличиях смотрите в видео:
Вероятностное прогнозирование спроса
Рассмотрим подробно, как работает вероятностная модель прогнозирования спроса. Предположим, что у нас есть исторические данные по продажам, и нужно оценить спрос на ближайшую неделю.
Сначала мы будем оценивать спрос на понедельник. Для этого случайным образом выбираем значение спроса за один из дней из истории продаж. Затем таким же образом выбираем из истории продаж значения спроса для вторника, среды, четверга и пятницы. Сложив их вместе получим пример спроса на неделю.
Периоды выборки могут меняться в зависимости от различных факторов. Например, если нужно учесть внутринедельную сезонность, то для прогнозирования будут использована выборка только определенных дней недели.
Это будет один эксперимент. Таких экспериментов мы обычно делаем более 100 000. В каждом эксперименте случайный выбор даёт разные значения дневных продаж, и в результате получаются разные недельные суммы. Вместе они образуют распределение спроса, показывающего вероятность определенных значений. Например:
- С 8% вероятностью будет продано 10 единиц товара
- С 7.5% вероятностью будет продано 12 единиц товара
- С 6.5% вероятностью будет продано 15 единиц товара
- и т.д.
Это очень упрощенная модель, но она дает общее понимание о работе алгоритма. В реальных условиях дополнительно нужно учитывает сезонность (ежегодную, ежемесячную, внутринедельную), промо-акции, праздники, вероятность возможных всплесков спроса, колебаний продаж и прочие факторы. Подробнее об этом можно прочесть в статье «14 факторов, которые нужно учитывать при прогнозировании товарных запасов».
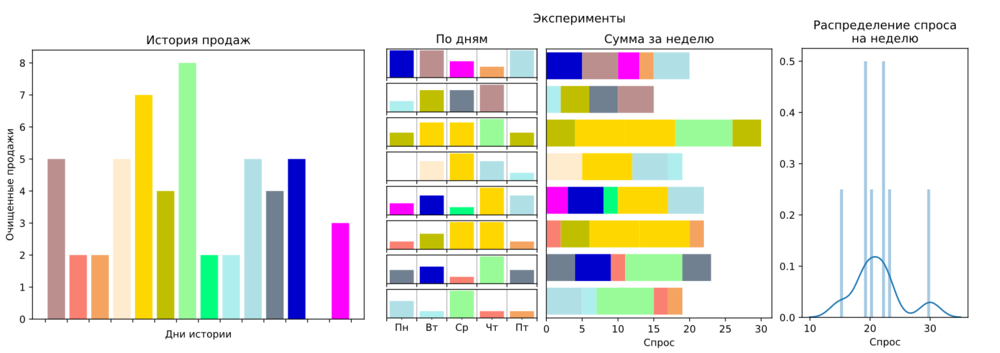
Рисунок 1. Моделирование спроса на неделю. Для упрощения показано 8 экспериментов. На первом графике изображена история продаж по дням за две недели. Второй график иллюстрирует результат восьми экспериментов. Каждая строка – отдельный эксперимент. В левой части графика – значение спроса по дням недели. В правой части – суммарный спрос за неделю. На третьем графике показано распределение вероятностей того или иного объема спроса.
Данная модель позволяет достаточно хорошо прогнозировать спрос с учетом требуемого уровня сервиса (I и II рода), оценивать риски и планировать запасы. Другими словами, зная прогноз спроса на будущий период, алгоритм знает, сколько нужно хранить товара, чтобы удовлетворить будущий спрос.
Сколько товара нужно заказать сегодня?
Как алгоритм, зная прогноз спроса, может понять, сколько нужно заказать товара? Для этого нужно учесть имеющиеся запасы (остатки) и заказы в пути, сделанные ранее .
Если на прогнозируемый период (его называют горизонт планирования) нет поступлений, то это сделать просто: достаточно вычесть из прогноза спроса текущие остатки на складе и сделать заказ на полученную величину.
Но зачастую мы имеем дело с регулярными ежедневными или еженедельными поступлениями товаров. Что делать в этом случае? Как, зная только спрос за какой-то период, можно понять, какой запас нам понадобится? Если оперировать прогнозом спроса на весь горизонт планирования, то есть всего два варианта.
Первый – взять объем товара в поступлении и вычесть его из планируемого спроса, как будто приходящее в будущем поступление уже лежит на нашем складе. Однако это может привести к дефициту. Другой вариант – не учитывать поступления вовсе. Но это может грозить перезатариванием.
Приведем пример:
Рассмотрим простой вариант, в котором значение спроса точно известно заранее. Пусть на товар имеется постоянный спрос 100 единиц в день. Рассчитывается заказ на одну неделю (5 дней). При этом исходно запасов товара на складе нет, но на пятый день приходит ранее сделанный заказ размером 300 единиц. Считаем, что запас становится доступным в день поступления.
Понятно, что для покрытия спроса надо заказать 400 единиц товара. Они покроют первые четыре дня, а дальше можно будет расходовать запас из поступления. К концу недели на складе останется 200 единиц товара.
Здесь возможны два варианта – учесть поступление 300 единиц товара так, как будто они будут доступны уже в первый день или не учитывать поступления совсем.
В первом случае для покрытия спроса на 5 дней в объеме 500 единиц будет сделан заказ на 200 единиц товара (поскольку считается, что 300 уже пришли). Однако этого объёма не хватит до поступления заказа, и на третий и четвертый день будет наблюдаться дефицит.
Во втором случае будет сделан заказ на все 500 единиц, и к концу недели останется уже не 200 единиц товара, а 300.
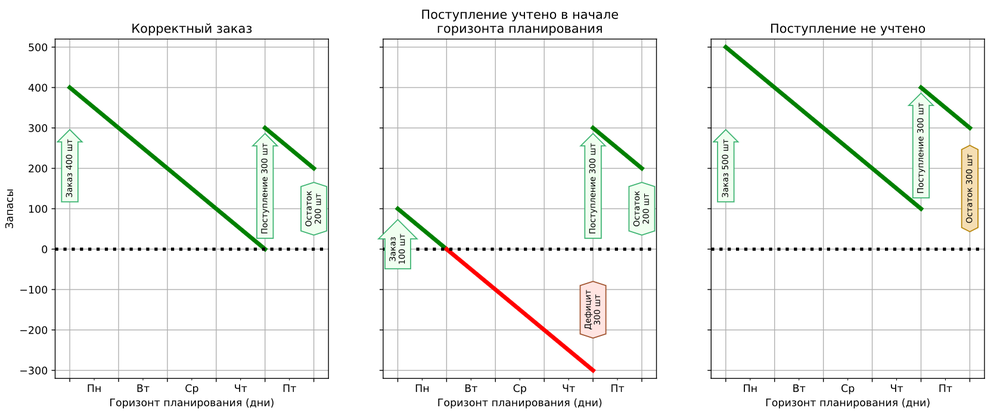
Рисунок 2. Разные варианты учёта известного поступления внутри горизонта планирования. На первом графике изображен корректный заказ (400 ед). Второй график иллюстрирует ситуацию, когда поступление (300 ед.) учтено так, будто уже доступно в первый день. На третьем графике ситуация, когда поступление не учитывается вовсе.
Оба варианта неидеальные. В реальных условиях с ежедневными поставками и большим количеством SKU такой подход может привести к большим финансовым потерям. Если же сократить период, на который прогнозируется спрос, то придется держать избыточный товарный запас, что тоже достаточно затратно.
Концептуальная ошибка здесь состоит в том, что, оперируя только прогнозом спроса на длительный период целиком, мы в принципе не можем учесть нюансы изменения товарных запасов на складе внутри этого периода. В рассмотренном примере объём заказа зависит от дня, в который станет доступно поступление. В примере это пятница, и нужно сделать заказ, который покрыл бы спрос с понедельника по четверг. Если бы поступление становилось доступным в среду, то достаточен был бы заказ на понедельник и вторник. А если поступление прибыло бы во вторник, то «идеальный" заказ должен был бы покрыть спрос понедельника и пятницы (так как поступления хватает на три дня).
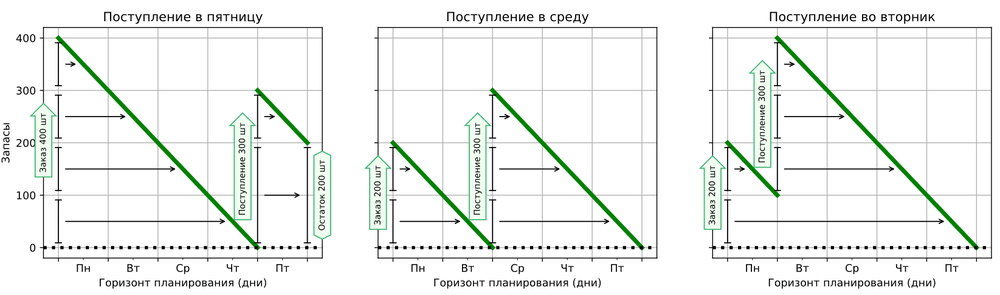
Рисунок 3. Корректный заказ при поступлениях 300 ед. в разные дни. Чтобы товара хватило на неделю, при поступлении в пятницу нужно заказать 400 ед, при поступлении в среду - 200 ед., при поступлении во вторник - 200 ед.
Получается, что в нашем простом примере, чтобы получить заказ, нужно сначала понять, спрос на какие дни из горизонта планирования покрывается поступлением, и сделать заказ на столько дней, сколько осталось не покрытыми. В случае постоянного спроса это несложно сделать, разделив общий прогноз пропорционально числу дней.
Но в общем случае спрос в разные дни может различаться под влиянием внутринедельной сезонности, маркетинговых акций или других факторов, и тогда делить спрос просто пропорционально числу дней будет некорректно. Да и определение того, на какую часть спроса нужно сделать заказ, в реальной ситуации тоже является нетривиальным: нужно учитывать уже имеющиеся запасы (которые могут состоять из нескольких партий с разным сроком годности), поступления в разные дни.
Из этих соображений видно, что расчёт заказа нельзя свести к простой арифметической операции вычитания. Необходимо полностью отслеживать возможную динамику изменения запасов на складе, на которую оказывают влияние как детерминированные факторы (например, объёмы поступлений или, наоборот, запланированных отгрузок клиентам, в конкретные даты), так и заранее неизвестный спрос, который оценивается вероятностно.
Прогнозирование товарных запасов
Главная задача эффективного управления запасами – определить, какое количество товаров должно быть на складе в определенный момент времени. Для этого недостаточно знать только суммарный прогноз спроса. Но умея моделировать величину спроса на произвольные периоды в будущем, мы можем уже говорить о прогнозировании товарных запасов и моделировании движения остатков на складе по дням. Если сможем моделировать, как будут изменяться остатки, то сможем точнее рассчитать заказ.
Зная прогноз спроса на период и количество товарных запасов на начала этого периода, мы может предположить, как быстро запасы будут уменьшаться, когда они станут равными нулю и когда возникнет дефицит. Дальше уже можно рассчитывать вероятности дефицита и т.д.
Как работает алгоритм подневного вероятностного моделирования запасов с учетом дат поступлений
Наша цель – спрогнозировать изменения остатков от начала до конца периода и понять, сколько товара будет храниться на складе каждый день, каков будет спрос, и хватит ли запасов для покрытия этого спроса.
Предположим, нужно сделать прогноз на следующий месяц. Но теперь моделирование спроса – это промежуточный этап, а на выходе из алгоритма мы будем оперировать прогнозом запасов.
Сначала строится прогноз спроса на первый день месяца. Для этого также используем случайное значение из статистики истории продаж за предыдущий период. Вычтя значение спроса из известного начального остатка получим прогноз товарного запаса на этот день. Далее таким же образом строятся прогнозы на второй, третий и последующие дни. Если в какой-то день должно прийти поступление, увеличим прогнозный запас на объем поступления. Полученную последовательность назовем траекторией. Это всего лишь один из сотен тысяч возможных вариантов развития событий – эксперимент, который показывает, как будут меняться остатки на складе по дням.
Если траектория в какой-то момент уходит в минус - это означает потребность в товаре. Именно на этот спрос необходимо рассчитывать заказ.
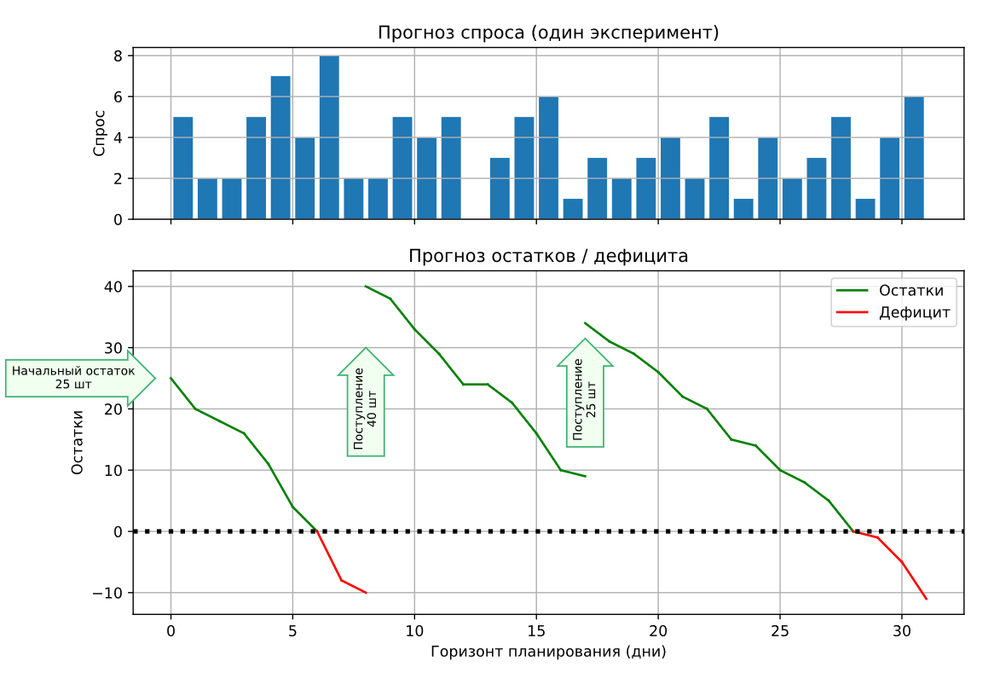Рисунок 4. Моделирование остатков для одного эксперимента.
Таких траекторий обычно строится более 100 000 для каждой товарной позиции. При моделировании учитываются промо-акции, сезонность, будущие поступления, вероятность дефицита, всплески спроса и прочие факторы. Имея огромный массив данных из более 100 000 возможных вариантов развития событий, можно определить вероятности возникновения дефицита разного объема, и, исходя из уровня сервиса и других параметров и ограничений, рассчитать заказ.
Работа с распределительным центром
Отдельно стоит поговорить про заказы через распределительный центр. Может показаться, что достаточно взять сумму очищенных продаж по филиалам, и этого будет достаточно для корректного расчёта заказа (Как очистить историю продаж за прошлый период).
В этом случае получится, что наш алгоритм прогнозирует спрос на всю сеть и не учитывает поступления и товарные остатки на конкретных филиалах.
Но тут тоже может возникнуть неточность. Даже если отслеживать изменение суммарных остатков во всей сети на каждый день, нельзя будет увидеть, что спрос возник на одном филиале, а запас, который вроде бы достаточен для покрытия этого спроса, находится на другом. Сложив остатки вместе и моделируя общий спрос мы уже не знаем, из каких компонентов они получены. Соответственно, может получится, что на одном филиале имеются излишки, и эти излишки не дают сделать заказ на другом филиале, на котором, напротив, имеется большой спрос, но нет запасов.
Эта задача достаточно сложная. При моделировании запасов нужно рассчитывать:
- Через сколько времени товар приедет от поставщика на РЦ
- Через сколько он будет на филиалах (учитываю, что они могут быть далеко друг от друга)
- Какие в это время будут промоакции, сезонность и факторы, влияющие на спрос
- Какой будет остаток на филиале на конкретную дату и как он будет меняться
- Когда и при каких условиях филиал сделает новый заказ
- Какой будет объем заказа, кратность, минимальная партия и прочие параметры
- Если один филиал делает заказ на РЦ, то нужно учесть остаток товара на РЦ и будущие заказы этого товара с других филиалов, после чего сделать заказ к поставщику. Иначе может получиться, что при заказе одного филиала сегодня, другой филиал уже не сможет заказать нужное количество товара через 2 дня.
Корректно решить эту задачу без учета движения остатков практически невозможно. В следующей статье мы расскажем, как работает алгоритм сквозного мультиэшелонного моделирования движения остатков через РЦ на филиалы.
