Расчет оптимального запаса товаров частого спроса с использованием нейронных сетей

Тверской государственный университет, Россия, г. Тверь 

В работе предложено использовать нейронные сети с определенной структурой для прогнозирования спроса на товары частого спроса и определения оптимального товарного запаса. Приведено сравнение с альтернативными методами прогнозирование, а также пример использования на действующем торговом предприятии.

Ключевые слова: управление товарными запасами; нейронные сети; прогнозирование спроса; частый спрос

Введение

В настоящий момент на оптово-розничных торговых предприятиях наблюдается проблема неэффективного использования оборотных средств. Большая часть оборотных средств торговых предприятий сосредоточена в товарных запасах. Для определения потребности в товаре и формирования заявки на заказ у поставщика используются достаточно простые и вместе с тем неточные модели прогнозирования спроса. В связи с этим по одним позициям наблюдается дефицит, в то время как по другим большой избыток. Согласно статистике ошибка при закупках по среднему может составлять до 381%. Все это ведет к нерациональному использованию денежных средств предприятия и складских помещений. Как следствие возникает просроченный товар, происходит снижение лояльности покупателей, заморозка оборотных средств, удорожание продукции. Согласно статистике, можно видеть, что запасы почти всех товаров растут с каждым годом.

В данной работе предлагается алгоритм определения товарного запаса с использованием нейронных сетей для товаров частого спроса. Под товарами частого спроса подразумеваются такие товары, для которых средний интервал между ненулевыми продажами больше 1.25 периода. Данный алгоритм являются частью разрабатываемого автором программного продукта для управления и оптимизации товарных запасов оптово-розничных торговых предприятий Forecast NOW!

Программный продукт позволяет в автоматическом режиме определять оптимальный метод прогнозирования спроса исходя из характеристик временного ряда спроса, размера доступной истории. Перед прогнозированием спроса производится восстановление спроса из ряда продаж, которое включает в себя фильтрацию аномальных продаж, восстановление спроса в моменты дефицита и маркетинговых акций, сглаживание спроса. После чего с учетом заданных внешних ограничений, таких как стоимость хранения, стоимость доставки, потери от дефицита, времени доставки, объема и габаритов транспортного средства, спроса на аналогичные товары и др. в автоматическом режиме производится расчет оптимального товарного запаса с точки зрения максимизации прибыли компании. Программный продукт позволяет проводить не только локальную оптимизацию товарных запасов при децентрализованном типе снабжения, но и полную оптимизацию всей цепи поставок при централизованном типе снабжения. В данной работе рассмотрим более подробно алгоритм определения товарного запаса с заданным целевым уровнем сервиса I рода с использованием нейронных сетей.

Расчет оптимального запаса с использованием нейронных сетей

Оптимальный запас Q рассчитывается как сумма прогнозируемого спроса D и страхового запаса S на случай колебания спроса и/или отклонения в сроках поставок.

Q=D+S 

Прогноз спроса рассчитывается с помощью нейронных сетей [1]. Искусственная нейронная сеть представляет собой систему нейронов и связей между ними (синапсов). Данная модель не программируется в привычном смысле, а обучается. Обучение заключается в предоставлении входного сигнала и сопоставлении выхода с ожидаемым его значением. В результате вычисляется отклонение реального выхода и желаемого, согласно которому корректируются существующие связи между нейронами. Корректировка осуществляется с использованием алгоритма обратного распространения ошибки. На каждой итерации происходит изменение параметров сети (весов связей и порогов активации нейронов) в направлении антиградиента ошибки. Известно, что такой подход обеспечивает сходимость к одному из локальных минимумов функции ошибки. С точки зрения математического моделирования происходит решение многопараметрической нелинейной задачи оптимизации. Пример полносвязной нейронной сети с двумя входами, одним выходом и скрытым слоем на 5 нейроном изображен на рисунке 1.
 

 

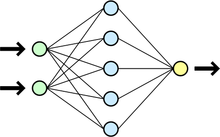
Рисунок 1. Схема нейронной сети с двумя входами
 

В нашем случае на вход нейронной сети подаются предыдущие продажи за 7 дней в случае краткосрочного прогнозирования или за 4-8 недель в случае долгосрочного, а также дополнительные факторы такие, как текущий день недели, номер недели в году, прогноз погоды и другие. На выходе нейронной сети ожидается получить прогнозируемое значение спроса на следующий день или неделю в зависимости от горизонта планирования. Возможность аппроксимации любой непрерывной функции с использованием нейронной сети показана в [2]. Таким образом, из имеющихся исторических данных подготавливается множество обучающих примеров для нейронной сети следующего вида

 

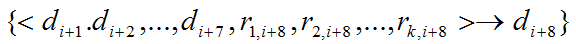
где   – значение спроса в i-ый день/неделю,  – значение k-го фактора в i-ый день/неделю.

Страховой запас s может быть рассчитан отдельно для колебания сроков поставок, неточности прогноза или с учетом двух факторов. Для расчета страхового запаса на случай неточности прогноза необходимо рассчитать ошибку прогнозирования RMSE [3] на прошлых данных по следующей формуле

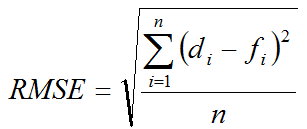
,где  - фактическое значение временного ряда спроса в i-ый день,  - прогнозируемое значение временного ряда спроса согласно обученной нейронной сети.

Для того чтобы рассчитать страховой запас на случай отклонения сроков поставок, нам необходимо рассчитать среднеквадратичное отклонение фактических прошлых сроков поставок CV(LT) по следующей формуле

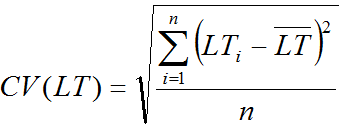
,где n  – количество поставок,   – i-ое время поставки,   – среднее время поставки

Пусть мы хотим обеспечить наличие товара на складе с заданным уровнем сервиса I рода SL, тогда при времени поставки LT, среднем спросе в единицу времени d получим следующую формулу для расчета оптимального запаса Q:

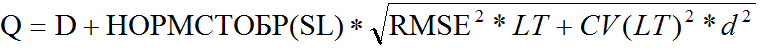
Расчет с учетом только колебаний спроса:

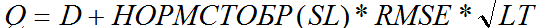
Расчет с учетом только колебаний сроков поставок

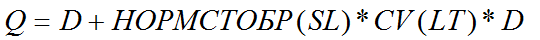
,где НОРМСТОБР  - функция обратного значения стандартного нормального распределения с математическим ожиданием равным нулю и дисперсией равной единице.

 
Сравнение с другими алгоритмами

Предлагаемый алгоритм и структура нейронной сети позволяет повысить точность прогнозов в среднем на 10-40% по сравнению с другими алгоритмами согласно протоколу проведенных испытаний. Сравнение проводилось с рядом методов и алгоритмов, включая методы прогнозирования AR, MA, ARIMA, EWMA, WMA, различные тренды, метод Хольта, Хольта-Винтерса и другие. Результаты сравнения представлены в таблице 1 и показывают насколько выше или ниже точность предлагаемого алгоритма по сравнению с альтернативными. В качестве параметров для сравниваемых методов выбирались такие параметры, которые дают наилучшее значение прогноза, что на практике невозможно. Параметры нейронной сети выбирались автоматически в процесс обучения.

Таблица 1. Сравнение точности с другими алгоритмами прогнозирования

 

Пример реального использования на продуктовой торговой компании и достигнутые результаты

Совместно с представителями одной из торговых сетевых компаний города Твери были выбраны 362 продукта для оценки эффективности работы предлагаемого алгоритма. Для тестирования была предоставлена база данных с историей продаж за 2 года и месяц. Продукты были выбраны таким образом, чтобы как можно более полно были представлены всевозможные случаи продаж разного рода:

• ярко выраженная недельная сезонность,
• наличие другой краткосрочной сезонности
• отсутствие краткосрочной сезонности
• наличие/отсутствие тренда,
• товары с высокой/низкой частотой продажи
• большие/низкие объемы среднесуточных продаж
• неслучайное отсутствие спроса,
• ограниченный спрос в условиях дефицита товара
• короткая история продаж (2-3 месяца)
• относительно длительная история продаж (более полугода)

Для каждого товара было построено 8 прогнозов, каждый на неделю. Таким образом, был смоделирован процесс работы пользователя с программой в течение 56 дней. Расписание приезда поставщиков соответствовало действительному. Качество прогноза оценивалось по ошибке SMAPE [4].

,где n – число точек во временном ряду,  – прогнозируемое значение,  – фактическое значение временного ряда в точке t.

Она рассчитывалась исключительно на прогнозируемом промежутке, что позволяет достичь объективности оценки в реальных условиях. Для расчета ошибки были получены реальные продажи на данном участке и вычислено абсолютное отклонение от прогноза в процентах.

Результаты по точности прогнозирования представлены в таблице 2.

Таблица 2. Точность прогнозирования для различных товаров

№ п/п	1	2	3	4	5	6	7	8	9	…	175	176
SMAPE	0,04	0,04	0,05	0,06	0,06	0,06	0,06	0,07	0,07		0,19	0,2
Точность	96,2	96,1	94,7	94,1	93,9	93,9	93,6	93,1	92,8	…	80,3	80,3
№ п/п	177	178	179	180	181	182	183	…	360	361	362	Среднее
SMAPE	0,2	0,2	0,2	0,21	0,21	0,21	0,21	…	0,32	0,32	0,32	0,19
Точность	80,3	80,2	80,1	80,0	79,8	79,7	79,7	…	68,2	68,1	68	80,3

Максимальная точность, которая была достигнута, составила 96,3%. Минимальная точность - 68%, а средняя – 80,3%. Среднеквадратичное отклонение составило 5%. Таким образом, основная масса товаров спрогнозирована с точностью от 75 до 85%. Точность выше 75% достигнута на 292 товарах из 362, что составляет 80% от общего числа товаров. Высокая ошибка получена преимущественно на тех товарах, у которых наблюдалась неожиданная смена тренда. Однако даже в таких условиях система показывает хорошую точность прогноза, составляющую порядка 70%. Точность прогнозирования может быть повышена за счет увеличения истории продаж. В этом случае могут быть учтены праздники, имеющие годовую сезонность (Новый Год, 8 марта и пр.).

Выводы

Имитационное моделирование проводилось на данных десяти предприятий России и СНГ. Моделировалось поведение склада и продаж при осуществлении закупок по рекомендациям программы в течение 3 месяцев в сравнении с реальными закупками. Общая расчетная экономия в процентном соотношении составляет 20-63% от общего объема склада.

Реальные внедрения в настоящий момент осуществлены на одиннадцати предприятиях России и СНГ, экономия соответствует имитационным планам, получены положительные отзывы от пользователей программного продукта.

Учитывая достигнутые результаты, можно рекомендовать использовать разработанный алгоритм для расчета оптимального размера запаса на оптово-розничных торговых предприятиях с частым спросом.

Список литературы

1. Хайкин С. Нейронные сети. Полный курс – 2-е изд., М.:Вильямс, 2006. – 114 c.
2. Cybenko G. Approximation by superpositions of a sigmoid function. – Mathematics of Control, Signals and Systems, vol. 2, 1989. – p. 303-314
3. Hyndman, Rob J. Koehler, Anne B. Another look at measures of forecast accuracy. – International Journal of Forecasting, 2006. – p. 679–688
4. Armstrong J. S. Long-range Forecasting: From Crystal Ball to Computer. – Wiley, 1978. – p. 2

 

DETERMINING OPTIMAL STOCK BALANCE FOR SMOOTH DEMAND USING NEURAL NETWORKS 

A.A. Gritsay

Tver State University, Russia, Tver 

In this paper we propose using neural networks to predict the demand for goods with frequent demand and determine the optimal stock balance. There is comparison with alternative methods of forecasting, as well as an example of use in a real business enterprise.

Ключевыеслова: inventory management; demand forecasting; neural networks; optimal stock

Об авторе:

ГРИЦАЙ Александр Александрович – магистр информационных технологий, аспирант направления «05.13.10 Управления в социальных и экономических системах», Тверской государственный университет (170000, г. Тверь, ул. Желябова, д. 33), e-mail: allgrit@forecastnow.ru

About the authors:

GRITSAY Alexander Alexandrovich – M.Sc. Informational Technology, postgraduate, Tver State University (33, Zhelyabova St., Tver, 170000), e-mail: allgrit@forecastnow.ru