Авторегрессия: формулы, примеры и ограничения

Авторегрессия — это один из самых простых и известных подходов к анализу временных рядов. Он широко применяется в статистике, экономике, логистике и прогнозировании спроса. В этой статье вы узнаете, что такое модель AR(1), как рассчитать прогноз по формуле, где авторегрессия работает хорошо, а где она ошибается. Мы также покажем, как AR используется в Forecast NOW! и почему её стоит применять с осторожностью.

Что такое авторегрессия

Что такое авторегрессия простыми словами? Это математический метод, при котором значение показателя в будущем рассчитывается на основе его предыдущих значений. Модель авторегрессии (AR, от англ. autoregressive model) — один из самых старых и популярных алгоритмов анализа временных рядов. Он прост, интерпретируем и широко используется в статистике, экономике, прогнозировании спроса и даже машинном обучении.

AR-модели особенно полезны, когда значения ряда демонстрируют устойчивость — например, в продажах товаров с регулярным стабильным спросом. Однако, как мы покажем дальше, они имеют ограничения и требуют аккуратного применения.

Определение авторегрессии

Авторегрессия — это модель, в которой текущее значение временного ряда зависит от его собственных предыдущих значений. То есть, вместо того чтобы опираться на внешние факторы или другие переменные, модель AR использует внутреннюю динамику самого ряда.

Формула авторегрессии (AR(p))

Авторегрессионная модель порядка p (обозначается как AR(p)) записывается так:

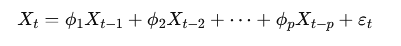
где:

• Xt​ — значение ряда в момент t,

• ϕ1,ϕ2,…,ϕp​ — коэффициенты модели,

• p — порядок авторегрессии,

• εt — ошибка модели (белый шум).

Если взять AR(1), то получим простейший вариант:

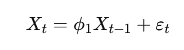
Это означает, что текущее значение зависит только от одного предыдущего значения.

Авторегрессия (AR, autoregression) — это алгоритм первого поколения, который может работать только на некоторых категориях товаров. Модель берёт историю продаж и ищет в ней закономерности: «если в прошлый раз был всплеск, то он, вероятно, повторится». Такой подход может быть полезен при достаточно стабильном спросе, без сильных колебаний и внешних воздействий.

В рамках системы Forecast NOW! проводилось тестирование этого алгоритма на реальных данных крупной продуктовой сети. Он показал хороший результат примерно на 6 % товарных позиций — тех, у которых продажи были относительно устойчивыми. Однако для остальных 94 % товаров — с сезонностью, акциями, завозами, сменами упаковок и пр. — результаты оказались неудовлетворительными. Подробнее можно ознакомиться по ссылке: fnow.ru/algorithm-comparison/avtoregressia

Важно понимать, что модель авторегрессии не учитывает внешний контекст: она не знает, что в магазине была выкладка, не различает причины роста спроса, не умеет учитывать аналоги и страховые запасы. Она лишь механически продолжает тренд, выявленный в прошлом.

Пример авторегрессии и формула AR

Чтобы лучше понять, как работает авторегрессия, рассмотрим простой пример и разберёмся, какую роль играет порядок модели.

Формула AR(1)

Простейшая авторегрессионная модель первого порядка — AR(1) — выглядит так:

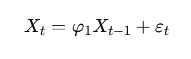
Здесь:

• X_t — значение в текущий момент времени,

• Xt−1 — значение за предыдущий период,

• φ1 — коэффициент авторегрессии,

• εt — случайная ошибка, белый шум.

Это означает: модель предсказывает текущее значение ряда на основе одного предыдущего. Чем выше φ1, тем сильнее влияние прошлого на будущее.

Как работает авторегрессия — простой пример

Представьте, что вы — менеджер магазина и хотите понять, сколько товара может продаться завтра. Вы замечаете закономерность: если вчера был высокий спрос, сегодня, скорее всего, он тоже будет высоким. Именно на этом принципе и строится модель авторегрессии: она смотрит на прошлые значения временного ряда и по ним прогнозирует будущее.

Допустим, у вас есть данные по продажам за три дня:

• 1-й день: 100 штук

• 2-й день: 105 штук

• 3-й день: 110 штук

• 4-й день: ❓ (нужно спрогнозировать)

Используем простую модель AR(1):

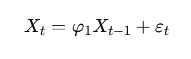
Где:

• φ1=0,9 — коэффициент, который показывает, насколько сильно текущее значение зависит от предыдущего;

• εt=3 — случайная ошибка, учитывающая внешние факторы.

Подставим данные:

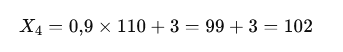
Прогноз на 4-й день: 102 единицы товара.

То есть модель делает вывод: «вчера продали 110, значит сегодня будет примерно 102, с учётом закономерности и случайных факторов».

Почему это может быть полезно?

Модель AR(1) проста, понятна и удобна, если спрос ведёт себя стабильно. Она не требует сложных вычислений и часто используется как базовая модель в статистике и логистике.

Но если спрос резко меняется — из-за акций, праздников, замены товара на аналог — такая модель может сильно ошибаться. В следующих разделах статьи мы рассмотрим, когда её стоит применять, а когда — лучше выбрать более продвинутый подход.

Что означает порядок модели AR(p)

Если модель обозначается как AR(3), это значит, что она учитывает три предыдущих значения: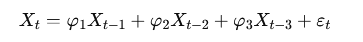

Чем выше порядок p, тем больше временных лагов учитывается. Но важно: увеличение порядка не всегда приводит к улучшению прогноза — особенно если ряд нестабилен или данные имеют сильный тренд или сезонность. Для подбора порядка часто используют графики автокорреляции (ACF/PACF), которые покажем дальше.

Когда использовать авторегрессию

Модель авторегрессии лучше всего работает в тех случаях, когда временной ряд стабилен и не имеет ярко выраженных трендов, сезонности или резких скачков. Такой ряд называют стационарным — это значит, что среднее значение и разброс данных остаются примерно одинаковыми на всём протяжении наблюдений.

Где авторегрессия применима

• Продажи товаров с постоянным спросом — например, базовые продукты питания без промо-акций;

• Заполнение регулярных отчётов (температура, давление, расход воды);

• Финансовые индикаторы при условии стабильного рынка.

В таких случаях модель AR способна выявлять закономерности и давать достаточно точный прогноз, не перегружая вычислениями.

Когда AR не подходит

• При акциях, промо-мероприятиях, изменении выкладки;

• При наличии сильной сезонности (например, новогодние товары);

• При частой смене SKU или упаковки;

• Для новинок, у которых нет истории продаж.

В этих ситуациях модель будет слепа к контексту и ошибаться, потому что ориентируется исключительно на значения в прошлом, не зная причин колебаний.

Ограничения AR и сравнение с другими моделями

Несмотря на простоту, авторегрессия — это лишь базовая модель, которая не справляется со сложным поведением спроса.

Ограничения AR

• Не учитывает внешние факторы — погоду, промо, конкуренцию;

• Не справляется с нестабильными SKU — всплески, дефицит, импульсные покупки;

• Требует стационарности ряда, что редко встречается в реальной торговле.

Поэтому в большинстве случаев AR проигрывает более гибким алгоритмам.

Ограничения точности AR: примеры и кейсы

Мы провели детальное сравнение точности прогноза авторегрессии с фирменным алгоритмом системы Forecast NOW!. В тестах для каждого товара подбиралась оптимальная AR-модель (перебором порядка AR с penalizацией за сложность модели) на исторических данных, затем сравнивались прогнозы AR и Forecast NOW! по метрике RMSE. Результаты однозначно показали, что почти во всех случаях алгоритм Forecast NOW! прогнозирует точнее AR-модели.

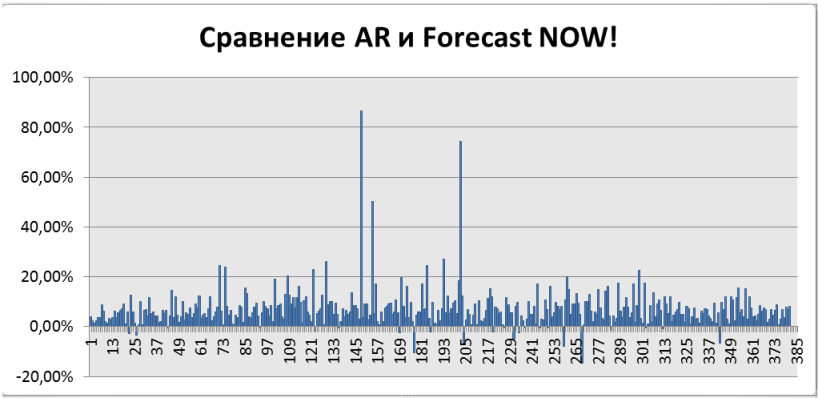
Как видно из графика и отчетов, Forecast NOW! превосходит AR примерно на 10–20% по точности прогнозов для большинства товаров. Лишь в считанных случаях (столбцы около нуля на графике) авторегрессия приблизилась по качеству, и практически нет примеров, где бы простая AR превзошла алгоритм Forecast NOW!. В среднем же прирост точности в пользу Forecast NOW! составил двузначные проценты. Более точный прогноз напрямую конвертируется в более грамотное планирование запасов и заказов, поэтому от использования чистой AR-модели для управления запасами создатели системы отказались.

В самой статье про авторегрессию показано, почему AR-модель часто либо недообучается, либо переобучается, что снижает ее практическую ценность. Например, модель AR(1) (первого порядка, учитывающая только вчерашние продажи) смогла воспроизвести лишь самые незначительные колебания спроса — ее прогноз фактически близок к среднему и не отражает существенных пиков. Очевидно, продажи определяются не только тем, что было продано за вчера или позавчера, поэтому AR(1) тривиальна и недостаточна для большинства товаров. С другой стороны, увеличение порядка AR повышает гибкость модели, но несет риск переобучения: если включить слишком много лагов, модель начнет подгоняться под шум и аномалии в данных. В статье отмечено, что при большом порядке AR «прогноз в качестве результата ничего хорошего не выдаст — модель просто запомнит все данные со всеми их недостатками и спрогнозирует не спрос, а проблемы со складом и резкие выбросы». Этот эффект продемонстрирован на примере: при увеличении порядка до 14 и 32 дней AR-модель идеально повторила почти все исторические пики, но качество прогноза даже ухудшилось — RMSE возрос с минимального значения 6.96 (на порядке ~7—8) до 7.03 и 7.45 соответственно. Таким образом, чрезмерно сложная AR-модель теряет обобщающую способность. Оптимум в том эксперименте пришелся на порядок p ≈ 7 (около недели предыдущих данных) — видимо, за счет учета недельной сезонности удалось выжать максимум информации, минимизируя шум. Дальнейшее увеличение лага только ухудшало точность прогноза.

Вывод из этих примеров: модель AR полезна лишь в узком диапазоне условий. Она может показывать приемлемые результаты, когда спрос действительно ведет себя как авторегрессия невысокого порядка — к примеру, имеет выраженную регулярность от периода к периоду (суточный, недельный цикл) и малую вариативность. В таких случаях даже простые методы (AR, скользящее среднее, экспоненциальное сглаживание) могут спрогнозировать близкое к среднему значение, а добавление нормального страхового запаса сработает корректно. Именно это наблюдалось для немногих товаров (~4—6%) с регулярным спросом, где и нейросетевые, и статистические алгоритмы давали отличные точечные прогнозы. Однако для подавляющего большинства SKU, имеющих разреженный или нерегулярный спрос (94–96% ассортимента), подход AR/ARIMA сильно проигрывает — модель либо не имеет достаточных данных для обучения, либо ее предположения о распределении спроса не выполняются. Например, в классических подходах часто предполагается нормальное или пуассоновское распределение спроса для расчета страхового запаса, но доказано, что эти распределения не описывают спрос ~94% товарных позиций. В итоге AR-модель для таких позиций дает низкую точность, а требуемый страховой запас приходится задавать «с запасом» (до 70% от объема запаса), что неэффективно. Таким образом, реальных кейсов, где AR-модель была бы однозначно полезна, весьма мало — разве что товары с абсолютно стабильной реализацией (условно, «молоко по 100 пачек каждый день»), для которых и простые методы примерно пригодны. Но даже в этих случаях Forecast NOW!, как правило, справляется не хуже, учитывая еще и дополнительные факторы.

Что такое ARMA и ARIMA

Чтобы устранить ограничения простой авторегрессии, в статистике используют:

• ARMA — авторегрессия + модель скользящего среднего (учёт прошлых ошибок);

• ARIMA — дополнительно включает компонент интегрирования, устраняющий тренд;

• SARIMA — добавляет сезонность.

Пример ARIMA(1,1,1): означает авторегрессию первого порядка + 1 раз дифференцированный ряд + скользящее среднее.

Модели и алгоритмы, используемые вместо AR

Вместо авторегрессии и иных моделей первого-второго поколения (таких как SMA, ES, Holt-Winters и пр.), Forecast NOW! применяет более современные, многокомпонентные подходы к прогнозированию и управлению запасами. Центральное место занимают вероятностные алгоритмы прогнозирования (алгоритмы 4-го поколения). В отличие от AR, выдающей единственное число прогноза, вероятностная модель генерирует распределение спроса. Проще говоря, Forecast NOW! имитирует тысячи возможных реализаций будущих продаж и на основе этой симуляции строит прогноз в виде распределения вероятностей различных объемов спроса. Например, алгоритм может показать, что вероятность продать 12 единиц товара составляет 7.5%, а 20 единиц — 15%. Такой подход кардинально отличается от классической авторегрессии и хорошо работает для всех типов товаров, включая позиции с редким или сильно колеблющимся спросом. Вместо неточного прогноза-точки мы получаем набор вероятностных оценок, на основании которых можно более эффективно управлять запасами. При этом отпадает необходимость рассчитывать страховой запас по упрощенным формулам — нужный уровень сервиса достигается за счет выбора соответствующего квантиля из прогнозного распределения.

Более того, в Forecast NOW! делается упор на комплексное моделирование запасов и процесса заказа, а не на отдельный прогноз спроса. Эффективнее всего сразу моделировать заказ поставщику, а не прогнозировать отдельно спрос и запас. То есть система имитирует движение товара на складе по дням с учетом всех ожидаемых поставок, текущих остатков, риска дефицитов, просрочек, акций, сезонности и прочих факторов, чтобы напрямую рассчитать оптимальный заказ и необходимый уровень пополнения. Такой подход фактически отвечает на главный вопрос управления запасами: сколько и когда заказывать, минуя стадию явного прогноза спроса по AR-модели. Преимущество подхода очевидно: зная вероятное поведение запаса на любую будущую дату, можно гораздо точнее определить необходимое количество для заказа и минимизировать издержки.

Кроме вероятностных алгоритмов, мы испытали и альтернативные методы, например нейронные сети и генетические алгоритмы. Интересно, что от нейросетей мы в Forecast NOW! тоже в итоге отказались. Причины оказались схожими с ограничениями AR: нейросеть обучается по историческим данным и выдает один прогноз (со всеми вытекающими проблемами необходимости страхового запаса и нечувствительности к редкому спросу). В практике Forecast NOW! самообучающиеся нейросети отлично себя показали лишь для тех же самых 4–6% товаров с регулярным спросом — по сути, для группы товаров, где и AR-модель могла бы сработать. Однако для 94–96% ассортимента с разреженными продажами нейросетям не хватало данных, да и рассчитанный по ним заказ все равно требовал корректировки на риск (ведь нормальное распределение для вариабельного спроса не применимо). Кроме того, внедрение нейросетей сильно усложняло систему (нужны тщательно очищенные данные, множество признаков, контроль от переобучения и прочее.). В результате команда сделала вывод, что probabilistic-алгоритмы имитированного моделирования дают более устойчивый и универсальный результат, чем AI/ML-подходы в задаче прогноза запасов.

Рекомендуем прочитать статью: "Почему мы отказались от использования нейросетей в прогнозировании?"

Подводя итог, Forecast NOW! заменяет AR-модель комплексом вероятностных и имитационных методов. Они позволяют учитывать: вариативность спроса, сезонность, промо-активности, поставки с разным интервалом и задержками, ограничения поставщиков, стоимость хранения и потери от дефицита или излишка — всё то, что остается «за кадром» при использовании одной лишь авторегрессии. Благодаря этим алгоритмам 4-го поколения система может эффективно работать даже с «тяжелыми» позициями группы Z (товары с очень редкими продажами), где классические методы бессильны. Отдельно стоит отметить, что отдел R&D компании постоянно отслеживает новейшие исследования и алгоритмы; все новшества проходят тестирование, и лучшие из них внедряются в Forecast NOW!. Это означает, что вместо опоры на устаревшую авторегрессию платформа использует наиболее эффективные на сегодняшний день модели для разных сценариев управления запасами.

Как построить AR-модель на практике

Авторегрессия считается одной из самых простых моделей прогнозирования, и её можно быстро реализовать с помощью Python. Но, как и в любой аналитике временных рядов, перед построением модели важно правильно подготовить данные.

1. Проверка стационарности (ADF-тест)

Прежде чем использовать AR-модель, необходимо проверить, является ли ряд стационарным — то есть, сохраняются ли его среднее значение и дисперсия во времени. Это критическое требование для корректной работы авторегрессии.

Для проверки используют ADF-тест (Augmented Dickey-Fuller). Если p-value теста < 0.05, ряд считается стационарным.

Пример в Python:from statsmodels.tsa.stattools import adfuller

result = adfuller(data)
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')Если ряд нестационарен, можно применить дифференцирование: data.diff().dropna().

2. Выбор порядка модели: ACF и PACF

Чтобы выбрать, сколько предыдущих значений учитывать (порядок модели p), строят два графика:

• ACF (автокорреляционная функция) — показывает, как текущее значение связано с прошлыми.

• PACF (частичная автокорреляция) — помогает точно определить порядок AR.

Пример построения:from statsmodels.graphics.tsaplots import plot_acf, plot_pacf

plot_acf(data)
plot_pacf(data)Если PACF резко обрывается после первого лага — вероятно, модель AR(1) будет достаточно точной.

3. Построение AR-модели в Python

Библиотека statsmodels позволяет быстро построить AR-модель:

from statsmodels.tsa.ar_model import AutoReg

model = AutoReg(data, lags=1)
model_fit = model.fit()
prediction = model_fit.predict(start=len(data), end=len(data))
print(prediction)

Здесь lags=1 соответствует модели AR(1). Вы можете подобрать оптимальное значение lags вручную, по PACF-графику или с помощью кросс-валидации.

После построения модели важно оценить её точность (MAE, RMSE) и проверить, не «уходит» ли она от фактических значений. 

Применение модели AR для прогнозирования спроса

Модель авторегрессии (AR) нами рассматривается как алгоритм первого поколения прогнозирования. Она опирается на предыдущие продажи для предсказания следующего периода, то есть линейно регрессирует будущее значение на несколько прошлых значений спроса. Подчёркивам, что такая модель пригодна лишь для товаров с гладким, регулярным спросом, что характерно примерно для 6% ассортимента типового продуктового супермаркета и практически не встречается в других отраслях. В остальных случаях простая AR-модель не дает достаточной точности. По этой причине мы не делаем ставку на чисто AR-прогнозирование спроса. Напротив, рекомендуется прогнозировать товарные запасы, а не спрос как таковой, используя более продвинутые подходы. Иными словами, в стандартных сценариях Forecast NOW! не применяет AR(1) или AR(p) как основной метод.

Подробнее можно ознакомиться по ссылке: fnow.ru/algorithm-comparison/avtoregressia

Важно отметить, что сами по себе классические методы прогнозирования (скользящее среднее, экспоненциальное сглаживание, ARIMA и др.), к которым относится и AR, считаются  устаревшими и малоэффективными для большинства SKU. Они дают лишь точечный прогноз спроса на следующий период и не учитывают многих факторов. В современных условиях практически не встретишь идеальную ситуацию со стабильными ежедневными продажами, когда можно было бы управлять запасами только на основе простого прогноза спроса.

Рекомендуем статью к прочтению: "Почему нужно прогнозировать товарные запасы, а не спрос?"

В жизни на спрос и потребность в товаре влияют задержки поставок, акции, сезонность, колебания покупательского спроса и прочие случайности — всего этого модель AR не учитывает напрямую. Таким образом, применение AR-модели в Forecast NOW! крайне ограничено случаем устойчивого, предсказуемого спроса, который встречается лишь у малого процента товаров (например, ежедневного спроса на базовые продукты питания). Для подавляющего большинства позиций (включая до 94% товаров даже в продовольственном ритейле и до 99% вне продуктовой сферы*) спрос является разреженным (нерегулярным), и прогнозировать его одной цифрой с помощью AR — все равно что стрелять вслепую по движущейся цели. 

В заключение: Авторегрессия (AR) — это простая и понятная модель, которая может быть полезной в ряде задач, особенно если вы только начинаете работать с временными рядами. Она хорошо объясняется, легко реализуется и быстро даёт прогноз. 

Когда AR уместна:

• При наличии длинной, чистой и ровной истории продаж;

• Для обучения студентов и начинающих аналитиков;

• В задачах, где важна интерпретируемость, а не максимальная точность;

Модель авторегрессии была исследована и признана эффективной только для очень ограниченного круга задач (гладкий спрос, короткий прогноз), поэтому в реальной работе системы её заменяют вероятностные алгоритмы и имитационное моделирование, обеспечивающие более высокую точность и надёжность решений. Точность AR отслеживается преимущественно для того, чтобы показывать клиентам и специалистам преимущество современных методов над традиционными. Такое сопоставление наглядно демонстрирует, что, хотя AR(1) или даже AR(7) может дать некий прогноз, для достижения максимальной эффективности управления запасами следует опираться на продвинутые технологии, например Forecast NOW!, а не на классическую авторегрессию. Это подтверждается и цифрами сравнительных тестов, и практическим опытом внедрения системы.