Уровень сервиса – важный показатель в управлении товарными запасами. Планируя его, мы понимаем, какую величину дефицита товара можем допустить, и в итоге определяем, сколько товара нужно хранить и заказать.
Рассчитывая его в прошлом, мы можем оценить, насколько эффективно мы удовлетворяли спрос.
Существует два типа уровней сервиса – I и II рода. Уровень сервиса I рода – это вероятность полного отсутствия дефицита за цикл поставки. Уровень сервиса II рода – доля спроса, которую мы гарантированно покроем с использованием имеющихся на складе запасов в течение периода их пополнения. Подробнее о том, чем отличаются уровни сервиса I и II рода и как их рассчитать, мы рассказывали в статье «Что такое уровень сервиса и почему он важен.
Зачем считать и планировать уровень сервиса
Для удовлетворения спроса и эффективного управления запасами нам важно понимать:
- Сколько спроса мы упустили, пока товара не было в наличии. Можем посчитать уровень удовлетворения спроса по разным товарам, товарным группам или торговым точкам.
- Какая величина дефицита товара может быть допустимой. Это необходимо для того, чтобы понимать, насколько хорошо или плохо мы управляем товарными запасами.
- Как запланировать уровень сервиса на будущее и управлять дефицитом. Если вы хотите поддерживать определЁнный уровень удовлетворения спроса, важно этим процессом управлять. Соответственно, вам нужно заложить какой-то уровень сервиса и, исходя из него, делать заказы.
- Как подобрать стратегии по управлению разными группами товаров. Для разных групп товаров будет разный уровень сервиса. Это логично: мы имеем дело с широким ассортиментом, все товары приносят разное количество прибыли, на них разный спрос и т.д. Соответственно, и подходы к установке уровня сервиса на будущий период разные.
- Как минимизировать потери от всех факторов. Прогнозировать уровень сервиса на будущее необходимо из критериев экономической эффективности. Чем более высокий уровень сервиса вы будете поддерживать, тем больше потеряете на хранении и обслуживании товара и увеличите риски списания. С другой стороны, чем меньше уровень сервиса, тем больше потерь по товарам от потенциального дефицита. Необходимо найти такую точку оптимума, где потери минимизируются, а прибыль будет максимальна.
Уровень сервиса в логистике: расчет уровня сервиса на будущее и управление дефицитом
Классические методы предполагают управление уровнем сервиса с помощью квантильного прогнозирования. Суть их в следующем: у вас есть статистика продаж за прошлый период, и на её основании вы делаете прогноз спроса. Но не одним числом, а некоторой интервальной оценкой – прогноз спроса+страховой запас. Страховой запас – это то, что закладывается на случай колебания спроса и сроков доставки. Именно в нём и «зашит» уровень сервиса в классическом подходе.
Посмотрим, как это выглядит, на примере.
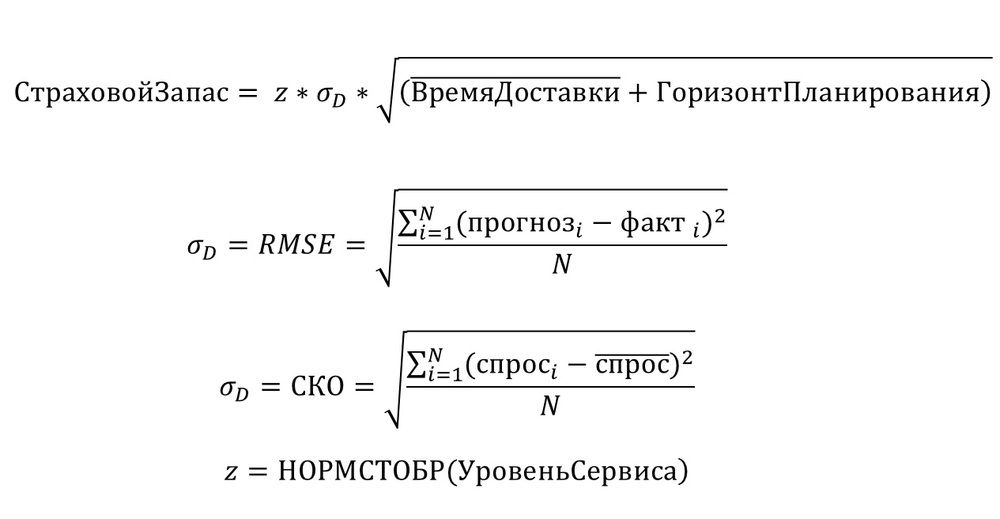
Перед вами классическая формула расчёта страхового запаса. Подробнее о том, как этот показатель рассчитать, можно прочитать в статье «Формула расчета страхового запаса» . Сейчас нам важен коэффициент Z. Именно он говорит про уровень сервиса первого рода или циклический уровень сервиса.
В классической модели, которая предполагает равномерное распределение спроса по всем товарам, Z исчисляется исходя из обратного нормального распределения:
Z=НОРМСТОБР
Если поставить коэффициент Z в формулу в Exel (функция НОРМСТОБР), мы получим конкретное число. Посмотрим на таблицу ниже: каждому уровню чисел соответствует свой коэффициент Z. Если мы хотим поддержать уровень сервиса 60%, получим коэффициент 0,25. Для поддержания 70% уровня сервиса коэффициент будет 0,524 и т.д.
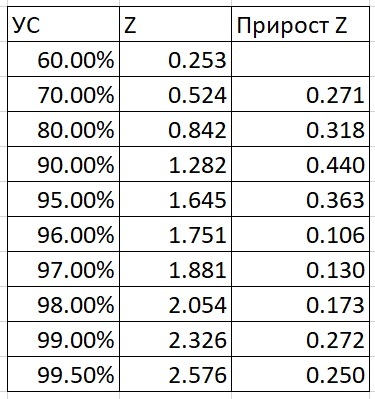
На этом примере видно: чем выше уровень сервиса, тем дороже он обходится. В диапазоне от 60% до 70% Z увеличился на 0,2, от 70% до 80% – на 0,31 и т.д. Диапазон всего в полпроцента с 99% до 99,5% даёт прирост Z на 0, 249. Практически такой Z у нас был на уровне от 60% до 70%. То есть с точки зрения страхового запаса нам будут одинаково стоить прирост Z на 10% (с 60% до 70%) и на полпроцента (с 99% до 99,5%). Для того чтобы обеспечить 100% уровень сервиса, нужны бездонные бюджеты и склады – идеальная ситуация, которой не может быть на практике.
Обращаем внимание: речь про уровень сервиса первого рода или циклический уровень сервиса. Здесь мы управляем не насыщением спроса, а дефицитными поставками. Если мы заложим 98% уровня сервиса и сделаем 100 поставок, это будет говорить о том, что в 98% случаев их хватит.
Управление уровнем сервиса II рода
Уровень сервиса II рода говорит нам не о ситуациях дефицита, а о насыщении спроса.
Формула страхового запаса будет такой же, но коэффициент Z для уровня сервиса II рода зависит от функции потерь L (partial expectation of backorders).
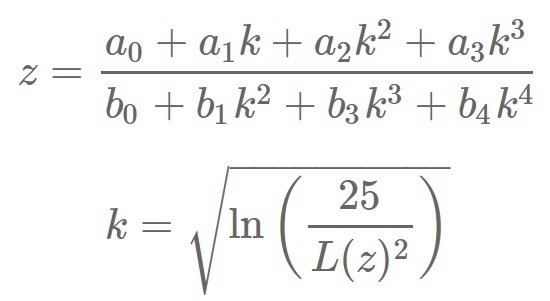
Проблема в том, что аналитического выражения этой функции не существует. В теории существуют таблицы нахождения Z по обратной стандартной функции потерь. Также используется метод аппроксимации Сильвера-Пайка Петерсона. Существует набор определённых коэффициентов, и по ним рассчитывается Z.
В этой статье мы не будем в них углубляться. Сейчас важнее понять другое: если у вас нет каких-то сложных функций, больших таблиц и большого набора коэффициентов, вы управляете уровнем сервиса I рода. То есть работаете на будущее не с упущенным спросом, а с вероятностью дефицита.
Если измерять эффективность того, чего вы хотите и чего достигли по прогнозам спроса и упущенным продажам уровня сервиса I рода, а планировать уровень сервиса II рода, это некорректно. Это не даст понимания, достигли ли вы того, что планировали. В этом главная проблема в управлении уровнем сервиса в классических моделях.
Сравнение уровня сервиса I и II рода
Посмотрим на изображение ниже. Коричневый график – это уровень сервиса I рода, синий – II рода.
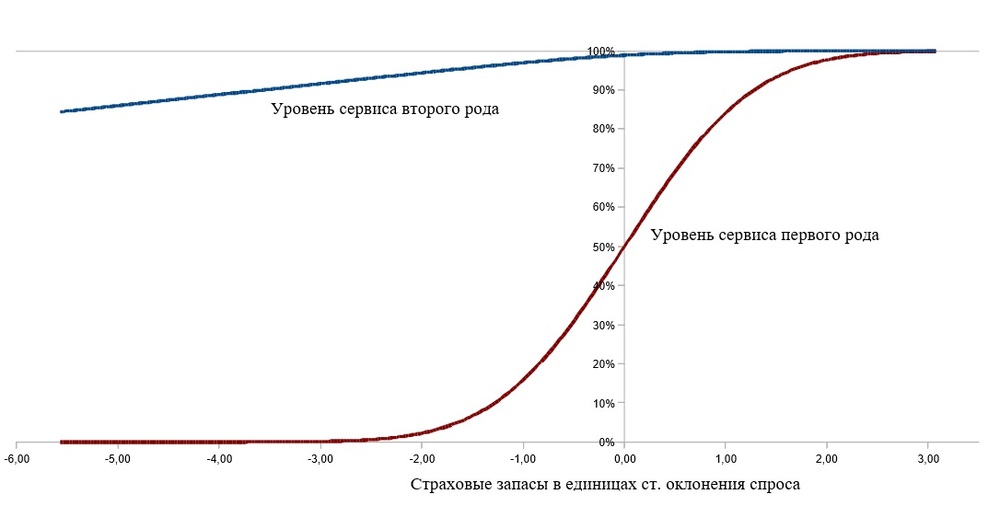
О чём нам говорит этот график?
Уровень сервиса II рода более плавный. Уровень сервиса I рода, наоборот, резко растёт – от 50% до 90%. Каждый следующий процент уровня сервиса II рода будет обходиться дороже. Например, чтобы обеспечить дополнительные 10% сервиса I рода от 60% до 70%, мы чуть-чуть увеличим страховой запас.
Для уровня сервиса II рода прирост страхового запаса будет существенным. При этом уровень сервиса II рода более плавный, по нему нет резких скачков и им проще управлять.
Напоминаем: важно понимать, каким уровнем сервиса вы пользовались в прошлом периоде и что планируете на будущее.
Почему классические модели управления уровнем сервиса не работают
О недостатках классических методов прогнозирования мы писали в статье «Обзор классических методов прогнозирования спроса» . Что касается управления уровнем сервиса, самый большой недостаток классических моделей в том, что на практике они не подходят для большинства позиций ассортимента. Такие способы применимы к товарам с гладкими продажами и нормальным распределением спроса. По нашим оценкам, это только 5%-10% товаров от общего ассортимента.
Модель уровня сервиса I рода, которую мы описывали выше, предполагает, что спрос по всем товарам обладает нормальным распределением. Если посмотреть на графике, нормальное распределение напоминает колокол.
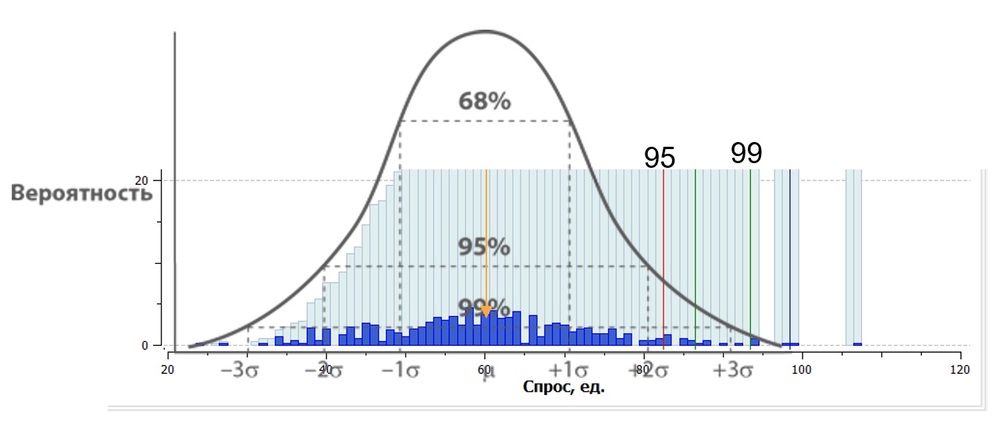
Допустим, у нас будет 100 фактов продаж. Самый частый из них – 50. 51 и 49 будут встречаться с одинаковой вероятностью, график будет уходить вправо и влево. На практике таким распределением обладают очень мало товаров. И даже у тех, что стабильно и ежедневно продаются, часто происходит смещение спроса.
Приведём пример: у нас есть ежедневные продажи товаров от 20 до 50. Казалось бы, небольшая вариативность. Но даже по ним распределение спроса на 1 день ненормальное. А если взять товары редкого спроса – автозапчасти, стройматериалы и 90% того, что продаётся в супермаркетах – продажи по ним могут варьироваться от 0 до 150 и т.д. У таких товаров не гладкий, хаотичный спрос. Применять к ним методы работы с товаром нормального распределения и прогнозировать уровень сервиса исходя из этих моделей – ошибка.
Если мы захотим поддерживать высокий уровень сервиса, то будем заказывать товаров больше чем нужно. Для низкого уровня сервиса есть обратный риск – недооценить запасы.
Рассмотрим ещё один пример. Перед вами график продаж бытовой химии.
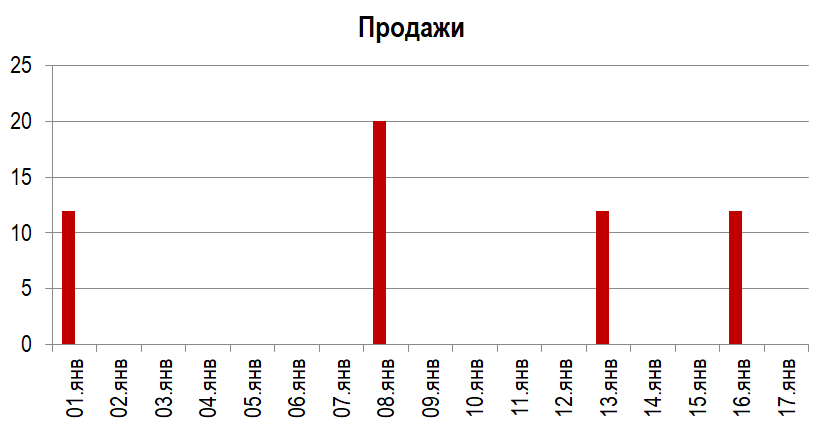
Мы видим хаотичные редкие продажи. Попробуем применить к ним модель классического прогнозирования.
Цель: уровень сервиса 87% (посчитали по формулам)
Будем хранить 10,35 штук средств для мытья посуды
По факту мы удовлетворим не 87%, а 71 % уровня сервиса.
Этот пример ещё раз доказывает, что для товаров редкого спроса методы прогнозирования страховых запасов, основанные на классических моделях нормального распределения спроса, не подходят. Решить проблему могут методы вероятностного прогнозирования.
Управление уровнем сервиса через вероятностное прогнозирование
Суть этого метода в том, что мы оцениваем спрос не одним числом, а набором вероятностей его возникновения. Мы построили вероятностные таблицы по продажам и знаем, какой спрос и с какой вероятностью у нас может настать. То есть считаем не одно число или интервал, а различные объёмы спроса и их вероятности, и потом принимаем экономически обоснованное решение.
Посмотрим на таблицу:
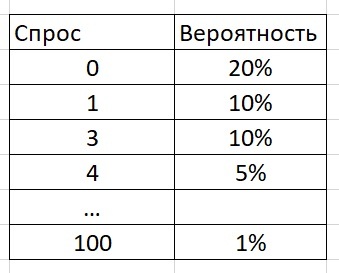Спрос 0 возникает с вероятностью 20%. Спрос 1 – с вероятностью 10% и т.д. По всем возможным значениям спроса посчитана вероятность их возникновения.
Дальше мы можем посчитать уровень сервиса I рода.
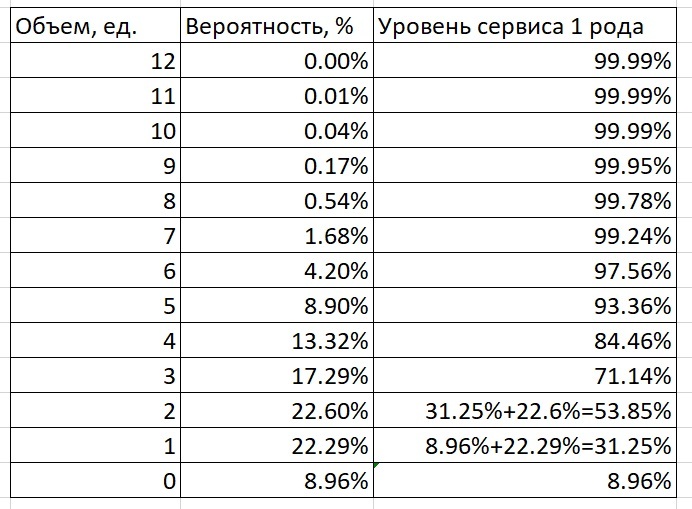У нас есть набор объёмов и набор вероятностей их возникновения. Спрос 0 возник в 9% случаев, спрос 1 – в 22, 3% случаев и т.д. Храня 0 штук продукции на складе, мы покроем 9% случаев. Поэтому уровень сервиса 1 рода у нас будет равен 8, 96%.
Храня 1 штуку на складе, мы покроем вероятности возникновения спроса 1 штуки (22,3%) и 0 штук (8,96%). Соответственно, храня 1 штуку, мы обеспечим уровень сервиса 31,25. Это вероятности возникновения нуля и единицы.
Храня 2 штуки, мы покроем возможный спрос для двойки, для единицы и для нуля: 8,96+22,29+22,6. То есть храня 2 штуки, мы покроем 53% случаев спроса и т.д.
Храня 6 штук, покроем 97,56% уровня сервиса (все вероятности спроса от 0 до 6) и обратно: чтобы обеспечить уровень сервиса I рода 97%, нужно хранить 6 штук.
Таким образом мы можем управлять уровнем сервиса первого рода в вероятностных моделях.
Как это реализовать в Exсel
Допустим, у нас есть ряд продаж, и мы хотим построить прогнозы спроса на два дня. В данном случае мы просто считаем, какой у нас спрос был за последние два дня. Сначала это 5, потом 0, затем 15 и т.д.
После необходимо понять, сколько раз встретился каждый объем спроса. В Exсel это делается с помощью функции СЧЕТЕСЛИ
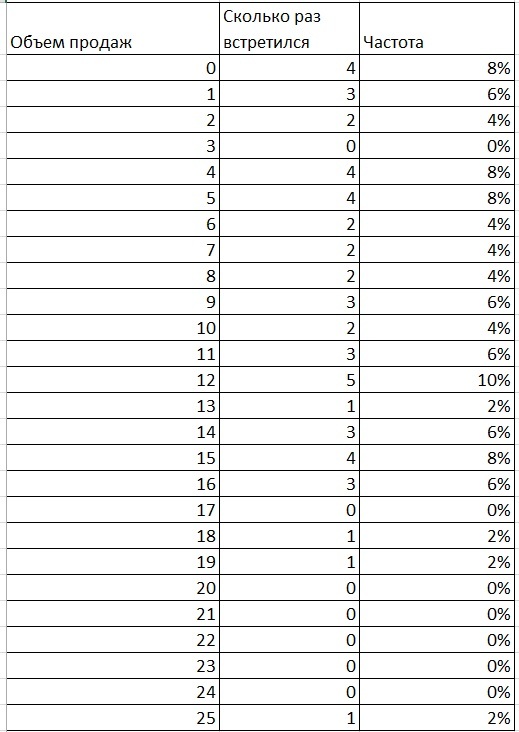Что мы видим: объём спроса 0 за 2 дня встретился 4 раза. Частота – это 8%. Продажа 1 встретилась в 6% случаев. Чтобы просчитать, какой уровень сервиса мы покрываем в этом случае, необходимо просуммировать вероятности. Храня 1 штуку, мы покроем 14% случаев. Уровень сервиса I рода у нас будет равен 14%.
Дальше протягиваем формулу и понимаем, какой запас какой уровень сервиса гарантирует. И соответственно – какой запас товара нужно хранить, чтобы поддержать определённый уровень сервиса.
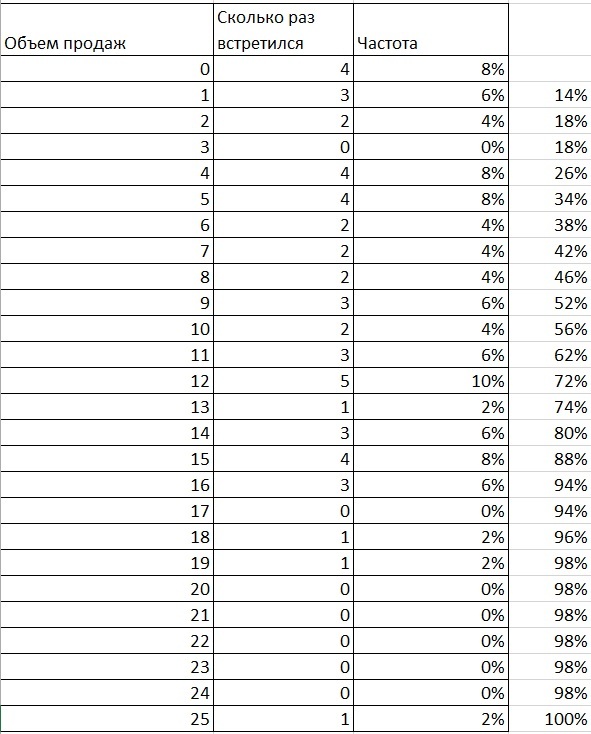Это простейшая модель, которую можно сделать в Exсel по вашим реальным продажам – здесь просто суммируются данные. Естественно, если вы хотите применять методы вероятностного моделирования, вам понадобится какой-то софт для подсчёта сложных вероятностных таблиц. Этот пример лишь помогает понять, как устроено управление уровнем сервиса I рода в моделях вероятностного прогнозирования.
Управление уровнем сервиса II рода
Об уровне сервиса II рода мы говорим, когда хотим управлять не дефицитными поставками, а насыщением спроса. То есть мы хотим гарантировать определенный процент удовлетворения спроса в будущем периоде, храня тот или иной объём запаса.
Вводные данные – те же. Таблица, где для каждого объёма спроса посчитана вероятность его возникновения.
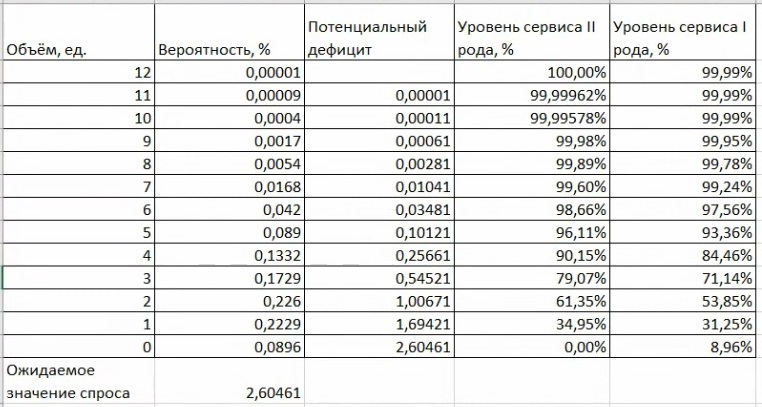
Далее необходимо посчитать математическое ожидание, то есть какой у нас спрос может быть исходя из этой таблицы вероятности. Для этого каждый объём спроса нужно умножить на вероятность его возникновения и сложить их между собой. В данном случае получаем число 2,6. (0*0,00896+1*0,2229+2*0,226+…+12*0,00001)
Далее нужно определить дефицит товара, который возникнет при хранении того или иного объёма запасов. Понятно, что если мы будем хранить 0 штук, то потенциально упустим наше ожидаемое значение спроса 2,6.
Посчитаем, какой спрос мы упустим, если будем хранить 1 штуку. Для этого необходимо упустить разницу между максимальным объёмом и единицей (12 – 1) и умножить получившееся число на вероятность возникновения этого спроса:
11х0, 00001
Далее прибавляем, сколько мы можем упустить при объеме 11:
11-1=10
10 штук мы упустим с вероятностью 0,00009. И так считаем для каждого объема запаса и продаж. Пример расчёта для единицы:
(12 – 1)х 0, 00001+(11-1)х 0, 0009+(10-1)х0, 00004 и тд.
Мы считаем, сколько спроса мы можем упустить, храня одну штуку товара. Для этого высчитаем значение спроса с текущим уровнем и умножаем на процент возникновения этого спроса. Для единицы получилось 1, 69. Чтобы посчитать упущенный спрос по двойке, мы берём все вероятности от 12 до 3 и по той же схеме.
Теперь мы можем рассчитать уровень сервиса II рода:
Ожидаемое значение спроса 2,6.
1,6 мы потенциально упустим
1,69/2,6 = 0, 65
100% - 65%= 35%
Для запаса 1 мы будем гарантировать уровень сервиса 2 рода почти 35%.
Если вы хотите гарантировать уровень сервиса 98%, необходимо хранить 6 штук товара. Хотите поддерживать 79% уровень сервиса, необходимо хранить 3 штуки. Обратите внимание: до уровня сервиса 99% уровень запасов будет равен 7. Если вы захотите увеличить его, то и прирост запасов будет существенным. Например, прирост уровня сервиса всего на 0,3% будет равен 1 штуке товара. Потом будет прирост уровня сервиса на 0,09% – это ещё одна штука товара. При этом для товаров хаотично и не стабильно продающихся каждый следующий процент и даже полпроцента до ста процентов уровня сервиса будут обходиться очень дорого.
Таким способом мы можем управлять уровнем сервиса 2 рода в методах математического моделирования. Как определить, какой уровень сервиса для того или иного товара необходимо поддерживать, мы расскажем в следующей статье.
